combinat::ribbonsTableaux – ribbon tableaux
The library combinat::ribbonsTableaux provides functions for generating and manipulating ribbon tableaux and their spin and cospin statistics. These objects are typed objects.
→ Examples
Creating Elements
combinat::ribbonsTableaux([inner, filling])
Parameters:
|
[inner, filling]:
|
The inner partition and the filling of each line listed from the top to the bottom (same convention as in combinat::tableaux).
|
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClassWith2DBoxedRepresentation
Axioms
Ax::canonicalRep
Related Domains:
combinat::partitions, combinat::skewPartitions, combinat::skewTableaux, combinat::tableaux
Details:
-
A 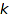 -ribbon tableaux ribTab is a partition or a skew partition (for more details see combinat::skewPartitions) filled with ribbons of length
-ribbon tableaux ribTab is a partition or a skew partition (for more details see combinat::skewPartitions) filled with ribbons of length 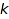 (for detail on ribbons see combinat::ribbons), and each ribbon is labelled with a non negative integer. The labels of each ribbon are placed on the diagonals of equations
(for detail on ribbons see combinat::ribbons), and each ribbon is labelled with a non negative integer. The labels of each ribbon are placed on the diagonals of equations 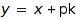 with
with 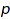 integer.
integer.
-
For a given ribbon, the tail is the lower right cell, the head is the upper left one and its evaluation is its label.
-
We also defined a semi-standard filling for a ribbon tableaux in this way: the head of a ribbon R must be at the right of a ribbon labelled with an integer less or equal than the evaluation of R, and the tail must be upon a ribbon labelled with an integer strictly less than the evaluation of R.
-
A ribbon tableau is said standard if all its ribbons are labelled with different integers from 1 to the number of ribbons in the tableau (if 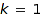 , ribbon tableaux are usual tableaux, see combinat::tableaux).
, ribbon tableaux are usual tableaux, see combinat::tableaux).
-
Here is an example of a 3-ribbon tableau of shape [[5,4,4,2,1],[2,1,1]] and evaluation [2,1,1]:
+--+
| |
+ +--+
|3 |
+--+--+--+--+
| 2 |
+--+--+--+
|1 | |
+--+ + +--+
| |1 |
+--+--+--+
-
The expression of a ribbon tableau is constituted by the inner partition of its shape and the list of its rows where the label of each ribbon is moved to its head position and zero everywhere else. For the previous example, the expression is [[2,1,1],[[3], [0,0], [2,0,0], [1,1,0,1],[0,0,0,0,0]]]. In order to create a ribbon tableau T call combinat::ribbonsTableaux with the expression of T.
-
On ribbon tableaux, we define a statistic spin as follows: we add the height minus 1 of each ribbon and divide the result by two. We also define the cospin of a ribbon tableau (the costatistic of the spin into the set of all ribbon tableaux of the same shape, weight and length) by computing the max of the spins of all ribbon tableaux of the same length, shape and evaluation minus its spin (this statistic is always a positive integer). For the previous example, the spin is 3/2.
-
With these two statistics we can define two generating polynomials of the set of all ribbon tableaux of a given shape, evaluation and length: they are called the spin and the cospin polynomials.
shape – the shape of a ribbon tableau
combinat::ribbonsTableaux::shape(ribbon tableau T)
Returns the shape of the ribbon tableau T.
evaluation – the evaluation of a ribbon tableau
combinat::ribbonsTableaux::evaluation(ribbon tableau T)
Returns the number of ribbons labelled with 1, labelled 2 and so on in the ribbon tableau T.
length – the length of the ribbons in a ribbon tableau
combinat::ribbonsTableaux::length(ribbon tableau T)
Returns the length of the ribbons in the ribbon tableau T.
spinTableau – the spin of a ribbon tableau
combinat::ribbonsTableaux::spinTableau(ribbon tableau T)
Returns the spin of the ribbon tableau T.
count – number of ribbon tableaux of a given length, shape and evaluation
combinat::ribbonsTableaux::count(partition shape, integer vector eval, integer 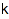 )
)
Returns the number of k-ribbon tableaux of shape shape and evaluation eval.
list – list all the ribbon tableaux of a given length, shape and evaluation
combinat::ribbonsTableaux::list(partition shape, integer vector eval, integer 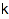 )
)
Returns all k-ribbon tableaux of shape shape and evaluation eval.
spinPolynom – the spin polynomial of the set of all ribbon tableaux of a given length, shape and evaluation
combinat::ribbonsTableaux::spinPolynom(partition shape, integer vector eval, integer 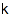 )
)
Returns the spin polynomial of the set of all k-ribbon tableaux of shape shape and evaluation eval.
cospinPolynom – the cospin polynomial of the set of all ribbon tableaux of a given length, shape and evaluation
combinat::ribbonsTableaux::cospinPolynom(partition shape, integer vector eval, integer 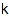 )
)
Returns the cospin polynomial of the set of all k-ribbon tableaux of shape shapeand evaluation eval.
StantonWhite – Stanton-White bijection
combinat::ribbonsTableaux::StantonWhite(ribbon tableau T)
Returns the k-tuple of semi-standard tableaux coming from the Stanton-White bijection.
fromStantonWhite – Stanton-White reverse bijection
combinat::ribbonsTableaux::fromStantonWhite(partition core, k-tuples of tableaux tabs)
Returns the k-ribbon tableaux corresponding to a given k-tuple of semi-standard tableaux.
Example 1:
Here, we demonstrate how to create a ribbon tableau as a typed object from its expression:
combinat::ribbonsTableaux([[2, 1], [[2], [0, 3], [0, 0, 0], [1, 0], [0]]])
+---+
| |
+ +---+
| 2 | |
+ + +---+
| | 3 |
+---+---+---+
| 1 |
+---+ +
| |
+---+
Example 2:
Counting the number of ribbon tableaux for right and skew shape:
combinat::ribbonsTableaux::count([6,6,6,6,6,6],[3,3,3,3],3)

combinat::ribbonsTableaux::count([[6,6,6,6,6,6],[3,3]],[4,4,2],3)

Example 3:
Listing 3-ribbon tableaux of evaluation [3,1] and shape the partition [5,4,3,2] which has as 3-core the partition [2]:
combinat::ribbonsTableaux::list([5, 4, 3, 2], [3, 1], 3)
-- +---+---+ +---+---+ +---+---+ --
| | 1 | | | 1 | | | 1 | | |
| + + +---+ + + +---+ + + +---+ |
| | | | 1 | | | | 2 | | | 2 | |
| + + + +---+ , + + + +---+ , + +---+---+---+ |
| | | 1 | | | | | 1 | | | | 1 | | |
| +---+---+ + +---+ +---+---+---+---+---+ +---+---+ + +---+ |
| | | 2 | | 1 | | | 1 | |
-- +---+---+---+ +---+---+---+ +---+---+---+ --
Example 4:
Listing 3-ribbon tableaux of skew shape [[6,6,6,6,6,6],[3,3,3]] and evaluation [5,4]:
combinat::ribbonsTableaux::list([[6, 6, 6, 6, 6, 6], [3, 3, 3]],
[5,4], 3)
-- +---+---+---+---+---+---+ +---+---+---+---+---+---+ +---+---+---+---+---+---+ --
| | | | 2 | | | 2 | | | 2 | | | 2 | | 2 | | | 2 | |
| + + + + + + + + +---+ + + + + +---+---+---+ + + + |
| | | 1 | | | 2 | | | | 1 | | | 2 | | | | 1 | | 2 | | |
| + + + + + + + + + +---+ + + + + +---+ + + + + |
| | 1 | | | 2 | | | | 1 | | 2 | | | | 1 | | 2 | | | |
| +---+---+---+---+---+---+, +---+---+---+---+---+---+, +---+---+---+---+---+---+ |
| | | | 1 | | | | 1 | | | | 1 | |
| + + + + + + + + + + + + |
| | | 1 | | | | 1 | | | | 1 | | |
| + + + + + + + + + + + + |
| | 1 | | | | 1 | | | | 1 | | | |
-- +---+---+---+ +---+---+---+ +---+---+---+ --
Example 5:
Finding the image of a given ribbon tableaux by the Stanton White bijection:
combinat::ribbonsTableaux::StantonWhite(combinat::ribbonsTableaux
([[],[[4,0,0,4,4,0],[3,3,0,0,0,0],[0,0,0,3,0,0],
[2,0,0,2,2,0],[1,1,0,0,0,0],[0,0,0,1,0,0]]]));
Warning: Uninitialized variable 'k' used;
during evaluation of 'combinat::skewPartitions::rQuotient'
-- -- +---+---+ +---+---+ +---+---+ -- --
| | | 4 | 4 | | 3 | 4 | | 3 | 3 | | |
| [], | +---+---+, +---+---+, +---+---+ | |
| | | 2 | 2 | | 1 | 2 | | 1 | 1 | | |
-- -- +---+---+ +---+---+ +---+---+ -- --
Example 6:
The first function computes the spin of a given tableau and the second one computes both the spin and the cospin polynomials for a given shape, evaluation and length:
combinat::ribbonsTableaux::spinTableau(combinat::ribbonsTableaux(
[[],[[4,0,0,4,4,0],[3,3,0,0,0,0],[0,0,0,3,0,0],
[2,0,0,2,2,0],[1,1,0,0,0,0],[0,0,0,1,0,0]]]));

combinat::ribbonsTableaux::spinPolynom([6, 6, 6, 6, 6, 6], [3, 3, 3, 3], 3);
combinat::ribbonsTableaux::cospinPolynom([6, 6, 6, 6, 6, 6], [3, 3, 3, 3], 3)

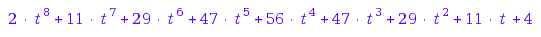
Background:
Ribbon tableaux were first introduced by Stanton and White for counting colored permutations. With spin or cospin polynomials we can defined two  -analogues of product of Schur functions. The specialization of these functions for some values of
-analogues of product of Schur functions. The specialization of these functions for some values of  provide conjectures for plethystic substitutions.
provide conjectures for plethystic substitutions.
Changes in MuPAD 3.1
New Function.
![]() -ribbon tableaux ribTab is a partition or a skew partition (for more details see combinat::skewPartitions) filled with ribbons of length
-ribbon tableaux ribTab is a partition or a skew partition (for more details see combinat::skewPartitions) filled with ribbons of length ![]() (for detail on ribbons see combinat::ribbons), and each ribbon is labelled with a non negative integer. The labels of each ribbon are placed on the diagonals of equations
(for detail on ribbons see combinat::ribbons), and each ribbon is labelled with a non negative integer. The labels of each ribbon are placed on the diagonals of equations ![]() with
with ![]() integer.
integer. ![]() , ribbon tableaux are usual tableaux, see combinat::tableaux).
, ribbon tableaux are usual tableaux, see combinat::tableaux).