combinat::skewTableaux – Young skew tableaux
The library combinat::skewTableaux provides functions for counting, generating, and manipulating Young skew tableaux.
→ Examples
Creating Elements
combinat::skewTableaux([inner, filling])
Parameters:
|
[inner, filling]:
|
The inner partition and the filling of each line listed from the top to the bottom (same convention as in combinat::tableaux).
|
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass
Axioms
Ax::systemRep
Related Domains:
combinat::skewPartitions
Details:
-
Let p be a skew partition of shape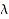 
. Recall that a skew partition can be depicted by a diagram of boxes (see combinat::skewPartitions). Fill now the boxes with numbers. Such a filling is a Young skew tableau, or, shorter, a skew tableau if the numbers in the boxes are non-decreasing along rows and (strictly) increasing from bottom to top along columns. The skew partition p is called the shape of the skew tableau. Recall that the shape of a skew partition is given by the outer partition and the inner partition (which is optional). Here is an example of skew tableau of shape [[5, 3, 1], [2, 1]]:
+---+
| 4 |
+---+---+---+
| 3 | 3 |
+---+---+---+---+
| 2 | 2 | 3 |
+---+---+---+
Moreover, if every positive integer up to the number of cases appears exactly once, the skew tableau is standard. Here is an example of standard skew tableau of shape [[5, 3, 1], [2, 1]]:
+---+
| 1 |
+---+---+---+
| 2 | 4 |
+---+---+---+---+
| 3 | 5 | 6 |
+---+---+---+
-
A skew tableau is encoded by the list of its shape's inner partition and the list of its rows, from top to bottom. For example, the above skew tableau is encoded by [[2, 1], [[1], [2, 4], [3, 5, 6]]].
Entries
|
"domtype"
|
The MuPAD domain used to represent tableaux: Type::ListOf(Type::Union(Type::ListOf(Type::NonNegInt), DOM_LIST)).
|
isASkewTableau – test if an object is a skew tableau
combinat::skewTableaux::isASkewTableau(skew tableau skt, <skew partition skp>)
Returns whether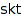 
is a skew tableau or not.
If the optional argument is present, returns whether skt is a skew tableau of shape skp or not.
isAStandardSkewTableau – test if an object is a standard skew tableau
combinat::skewTableaux::isAStandardSkewTableau(skew tableau skt, <skew partition skp>)
Returns whether skt is a standard skew tableau or not.
If the optional argument is present, returns whether skt is a standard skew tableau of shape skp or not.
toChain – return a given skew tableau as a chain of partitions
combinat::skewTableaux::toChain(skew tableau skt)
this function returns the chain of partitions corresponding to a given skew tableau standard or semi standard
fromShapeAndWord – skew tableau from its shape and natural reading
combinat::skewTableaux::fromShapeAndWord(skew partition shape, word w)
Returns the filling of the shape whose natural reading is the word w. Be careful: the result is not necessarily a skew tableau.
count – number of standard skew tableaux
combinat::skewTableaux::count(skew partition skp)
Returns the number of standard skew tableaux of shape skp.
list – list of standard skew tableaux
combinat::skewTableaux::list(skew partition skp)
Returns the list of the standard skew tableaux of shape skp. We use linear extension of the graph which represents the partial order between skew tableau cases.
generator – generator for standard skew tableaux
combinat::skewTableaux::generator({skew, partition, skp})
Returns a generator for the standard skew tableaux of shape skp.
Example 1:
These are two examples of skew tableau test:
combinat::skewTableaux::isASkewTableau([[3, 2] , [[4, 4], [1, 2, 4]] ]);
combinat::skewTableaux::isASkewTableau([[3, 1, 1] , [[4, 4], [1, 2, 4]] ]);
These are two examples of standard skew tableaux test:
combinat::skewTableaux::isAStandardSkewTableau([[2, 1], [[1], [2, 4], [3, 5, 6]]]);
combinat::skewTableaux::isAStandardSkewTableau([[2, 1], [[1], [2, 4], [3, 5, 7]]]);
Example 2:
There are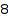 
skew tableaux of shape the skew partition 
:
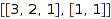combinat::skewTableaux::count([[3, 2, 1], [1, 1]])
Here is the list:
combinat::skewTableaux::list([[3, 2, 1], [1, 1]])
-- +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | 1 | | 1 | | 2 | | 2 | | 3 | | 4 | | 3 |
| +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+
| | 3 | , | 4 | , | 3 | , | 4 | , | 2 | , | 2 | , | 4 | ,
| +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+
| | 2 | 4 | | 2 | 3 | | 1 | 4 | | 1 | 3 | | 1 | 4 | | 1 | 3 | | 1 | 2 |
-- +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+ +---+---+
+---+ --
| 4 | |
+---+---+ |
| 3 | |
+---+---+ |
| 1 | 2 | |
+---+---+ --
If you want to run through the skew tableaux of a shape, you can generate them one by one to save memory:
g := combinat::skewTableaux::generator([[3, 2, 1], [1, 1]]);
g(); g(); g(); g(); g(); g(); g(); g(); g();
+---+
| 1 |
+---+---+
| 3 |
+---+---+
| 2 | 4 |
+---+---+
+---+
| 1 |
+---+---+
| 4 |
+---+---+
| 2 | 3 |
+---+---+
+---+
| 2 |
+---+---+
| 3 |
+---+---+
| 1 | 4 |
+---+---+
+---+
| 2 |
+---+---+
| 4 |
+---+---+
| 1 | 3 |
+---+---+
+---+
| 3 |
+---+---+
| 2 |
+---+---+
| 1 | 4 |
+---+---+
+---+
| 4 |
+---+---+
| 2 |
+---+---+
| 1 | 3 |
+---+---+
+---+
| 3 |
+---+---+
| 4 |
+---+---+
| 1 | 2 |
+---+---+
+---+
| 4 |
+---+---+
| 3 |
+---+---+
| 1 | 2 |
+---+---+
Typically, this would be used as follows:
g := combinat::skewTableaux::generator([[3, 2, 1], [1, 1]]):
while (p := g()) <> FAIL do print(p): end:
+---+
| 1 |
+---+---+
| 3 |
+---+---+
| 2 | 4 |
+---+---+
+---+
| 1 |
+---+---+
| 4 |
+---+---+
| 2 | 3 |
+---+---+
+---+
| 2 |
+---+---+
| 3 |
+---+---+
| 1 | 4 |
+---+---+
+---+
| 2 |
+---+---+
| 4 |
+---+---+
| 1 | 3 |
+---+---+
+---+
| 3 |
+---+---+
| 2 |
+---+---+
| 1 | 4 |
+---+---+
+---+
| 4 |
+---+---+
| 2 |
+---+---+
| 1 | 3 |
+---+---+
+---+
| 3 |
+---+---+
| 4 |
+---+---+
| 1 | 2 |
+---+---+
+---+
| 4 |
+---+---+
| 3 |
+---+---+
| 1 | 2 |
+---+---+
Example 3:
The skew tableau can be reconstructed back from the shape and the word:the result is not necessary a standard skew tableau, it depends on the word
combinat::skewTableaux::fromShapeAndWord([[3, 2, 1], [1, 1]], [1, 3, 4, 6]);
+---+
| 1 |
+---+---+
| 3 |
+---+---+
| 4 | 6 |
+---+---+
Example 4:
The skew tableau can be printed on screen with pretty form
combinat::skewTableaux::printPretty([[1, 1], [[1], [3], [4, 6]]]);
+---+
| 1 |
+---+---+
| 3 |
+---+---+
| 4 | 6 |
+---+---+