combinat::partitions – partitions of an integer
The library combinat::partitions provides functions for counting, generating, and manipulating partitions.
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::IntegerListsLexClass
Axioms
Ax::systemRep
Related Domains:
combinat::compositions, combinat::tableaux
Details:
-
A partition p of a nonnegative integer n is a non-increasing list of positive integers (the parts of the partition) with total sum n.
-
All functions for counting and generating accept the following optional constraints on the partitions: MinLength, MaxLength, Length, MinPart, MaxPart, Inner, Outer, MinSlope, and MaxSlope. Cf. examples 2, 3, 4, 5, 6, and 8.
-
A partition can be depicted by a diagram made of rows of boxes, where the number of boxes in the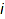 
-th row starting from the bottom is the 
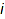-th part of the partition. For example, this is the diagram of the partition [5,3,1]: combinat::partitions::printPretty([5,3,1])
+---+
| |
+---+---+---+
| | | |
+---+---+---+---+---+
| | | | | |
+---+---+---+---+---+
Applying a reflection w.r.t. the main diagonal to this diagram yields the diagram of the conjugate partition, here [3,2,2,1,1]:
+---+
| |
+---+
| |
+---+---+
| | |
+---+---+
| | |
+---+---+---+
| | | |
+---+---+---+
See combinat::partitions::conjugate.
-
The coordinate system related to a partition applies from bottom to top and from left to right, so the corners of the partition [5,3,1] are [[1, 5], [2, 3], [3, 1]].
Entries
|
"domtype"
|
The MuPAD domain used to represent partitions: DOM_LIST
|
isA – test if an object is a partition
combinat::partitions::isA(any type part, <nonnegative integer n, constraints>)
Returns whether part is a partition.
If the optional argument n is present, returns whether part is a partition of n.
If constraints are given, returns whether part is a partition satisfying constraints.
count – number of partitions
combinat::partitions::count(nonnegative integer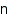 
, <constraints>)
Returns the number of partitions of n satisfying constraints.
generator – generator for partitions
combinat::partitions::generator(nonnegative integer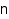 
, <constraints>)
Returns a generator for the partitions of n satisfying constraints.
list – list of the partitions
combinat::partitions::list(nonnegative integer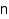 
, <constraints>)
Returns the list of the partitions of n satisfying constraints.
first – first partition
combinat::partitions::first(nonnegative integer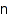 
, <constraints>)
Returns the first partition of n satisfying constraints or FAIL if there is none.
Next – next partition
combinat::partitions::Next(partition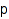 
, <constraints>)
Returns the partition following p satisfying constraints or FAIL if there is none.
printPretty – graphic representation of a partition
combinat::partitions::printPretty(partition p)
Returns a graphic representation of the partition as rows of boxes.
printCompact – graphic representation of a partition
combinat::partitions::printCompact(partition p)
Same as above, but in a more compact way, where each box is represented by #.
conjugate – conjugate of a partition
combinat::partitions::conjugate(partition p)
Returns the conjugate (or transposed) of the partition p. Geometrically, this operation amounts to a reflection of the diagram of the partition with respect to the main diagonal.
hookLengths – hookLengths of a partition
combinat::partitions::hookLengths(partition p)
Returns the list of the hook-lengths of the partition in the order of the row-reading from the topp.
These lengths allow to enumerate standard Young tableaux of shape p. The formula was first discovered by Frame, Robinson, and Thrall in 1954.
hookLengthInner – restricted hook length inner partition
combinat::partitions::hookLengthInner(partition p, integer k)
Returns the inner partition consisting of those cells of p whose hook lengths in p are strictly bigger than k.
Complexity: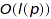 
, where 
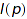is the number of parts of 
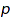(optimal).
toExp – exponential notation of a partition
combinat::partitions::toExp(partition p)
combinat::partitions::toExp(partition p, nonnegative integer k)
Returns the exponential notation of the partition p. This is a vector v of nonnegative integers such that v[i] counts the number of occurrences of i as a part of p. By default, the length of the vector is the size of the maximal part of p.
Returns the exponential notation of the partition p, padded with zeroes to ensure a length at least k.
See also combinat::partitions::fromExp.
fromExp – partition from its exponential notation
combinat::partitions::fromExp(list l)
Returns the partition p from its exponential notation l.
See also combinat::partitions::toExp.
centralizerSize – size of the centralizer of a permutation
combinat::partitions::centralizerSize(partition p)
Returns the size of the centralizer of any permutation with cycle-type p (see combinat::permutations::cycleType).
This is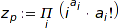 
, where 
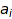denotes the number of parts 
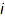in the partition 
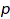(see combinat::partitions::toExp).
Those numbers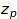 
play an important role in the theory of symmetric functions (see examples::SymmetricFunctions).
z – MacDonald's z numbers
combinat::partitions::z(partition p)
See combinat::partitions::centralizerSize.
conjugacyClassSize – size of a conjugacy class of the symmetric group
combinat::partitions::conjugacyClassSize(partition p)
Returns the size of the conjugacy class of the symmetric group indexed by the partition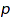 
, that is the number of permutations with cycle type 
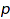(see combinat::permutations::cycleType).
This number is given by the formula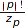 
(see combinat::partitions::centralizerSize).
Reference: A. Kerber, "Algebraic Combinatoric Via Finite Group Action", 1.3 p. 24.
corners – corners of a partition
combinat::partitions::corners(partition p)
Returns a list of coordinates of the corner boxes of the partition.
printPrettyCorners – graphic representation of the corners of a partition
combinat::partitions::printPrettyCorners(partition p)
Returns a graphic representation of the partition as rows of boxes where the corners are marked with *.
printCompactCorners – graphic representation of the corners of a partition
combinat::partitions::printCompactCorners(partition p)
Same as above, but in a more compact way, where each box is represented by # and corners are marked with *.
rCore – the r-core of a partition
combinat::partitions::rCore(partition part, nonnegative integer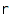 
)
Returns the r-core of a partition, ie the partition we obtain by retiring all ribbons from the partition. The set of all the r-core is a set strictly smaller than the set of all the partitions.
rQuotient – the r-quotient of a partition
combinat::partitions::rQuotient (partition part, nonnegative integer r)
Returns the r-quotient of a partition, ie a r-uplet of partitions.
fromCoreAndQuotient – partition from its core and its quotient
combinat::partitions::fromCoreAndQuotient(partition core, list of partitions lp)
Rebuilding the partition between its r-core and its r-quotient.
addVerticalRibbonStrip – Adding some ribbons to a partition
combinat::partitions::addVerticalRibbonStrip(partition part, list of nonnegative integers pos)
This function adds a ribbon to the partition 
for each non-zero entries of the vector 
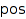. The length of the added ribbon is given by the value of the corresponding entry. By convention the first entry corresponds to the first line of the partition. This function returns the shape of the new partition and also the cumulative spin of the added ribbons.
removeVerticalRibbonStrip – Removing some ribbons in a partition
combinat::partitions::removeVerticalRibbonStrip(partition part, list of nonnegative integers pos)
This function removes a ribbon to the partition 
for each non-zero entries of the vector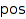 
. The length of the removed ribbon is given by the value of the corresponding entry. By convention the first entry corresponds to the first line of the partition. This function returns the shape of the new partition and also the cumulative spin of the removed ribbons.
jacobiTrudy – Jacoby-Trudi formula
combinat::partitions::jacobiTrudy(partition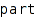 
, <function f>, <domain coeffRing>)
This function computes the Jacobi-Trudy matrix associated to the partition part. Its determinant express the Schur polynomial associated to part on the basis of homogenous complete symmetric polynomials (see Macdonald I.-G., (1995), "Symmetric Functions and Hall Polynomials", Oxford Science Publication). By default the function argument is i -> h[i] and coeffRing is Dom::ExpressionField(). These two options allow to obtain matrix entries as true symmetric functions.
contains – tests if one partition contains another
combinat::partitions::contains(partition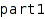 
, partition part2)
This function returns TRUE if both part1 and part2 are both partitions and part2 is contained in part1 (that is, each part of part2 is weakly smaller than the corresponding part of part1).
lequalYoungLattice – equivalent to the function contains
Example 1:
There are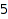 
partitions of 
:
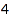combinat::partitions::count(4)
Here is the list:
combinat::partitions::list(4)
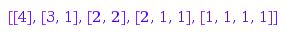
And here is the graphic representation of these partitions:
map(combinat::partitions::list(4), combinat::partitions::printPretty)
-- +---+ --
| | | |
| +---+ +---+ |
| | | | | |
| +---+ +---+---+ +---+ +---+ |
| | | | | | | | | | |
| +---+---+---+---+ +---+---+---+ +---+---+ +---+---+ +---+ |
| | | | | |, | | | |, | | |, | | |, | | |
-- +---+---+---+---+ +---+---+---+ +---+---+ +---+---+ +---+ --
Or in a more compact way:
map(combinat::partitions::list(4), combinat::partitions::printCompact)
-- # --
| # ## # # |
| ####, ###, ##, # , # |
-- ## # --
You can use the function combinat::partitions::first to get the “first” partition of a number:
combinat::partitions::first(4)
Using combinat::partitions::Next, you can calculate the “next” partition. This function takes as argument the partition relative to which you want the next one:
combinat::partitions::Next([4])
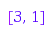
combinat::partitions::Next returns FAIL when the input is the last partition:
combinat::partitions::Next([1, 1, 1, 1])
When you want to run through the partitions of a number, you can generate them one by one to save memory:
g := combinat::partitions::generator(4):
g(); g(); g(); g(); g(); g()
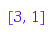
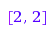
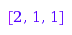
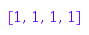
Typically, this would be used as follows:
g := combinat::partitions::generator(4):
while (p := g()) <> FAIL do print(p): end:
[4]
[3, 1]
[2, 2]
[2, 1, 1]
[1, 1, 1, 1]
Example 2:
The options Length, MinLength, and MaxLength can be used to set length constraints. This is the list of the partitions of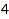 
of length 
:
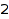combinat::partitions::list(4, Length=2)
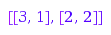
This is the list of the partitions of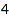 
of length at least 
:
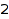combinat::partitions::list(4, MinLength=2)
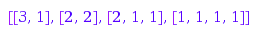
This is the list of the partitions of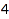 
of length at most 
:
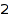combinat::partitions::list(4, MaxLength=2)
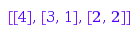
Setting both MinLength and MaxLength to the same value is equivalent to setting Length to this value. This is again the list of the partitions of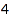 
of length 
:
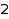combinat::partitions::list(4, MinLength=2, MaxLength=2)
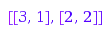
Example 3:
The options MinPart and MaxPart can be used to set constraints on the sizes of all parts. Using MaxPart, you can select partitions having only small entries. This is the list of the partitions of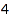 
with all parts at most 
:
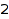combinat::partitions::list(4, MaxPart=2)
MinPart is complementary to MaxPart and selects partitions having only large parts (it takes a non-negative value). This is the list of the partitions of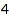 
with all parts at least 
:
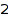combinat::partitions::list(4, MinPart=2)
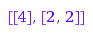
By default, the parts of a partition have to be positive. This can be changed using the option MinPart. In the following example, the options Length and MinPart are combined together to obtain the list of the partitions of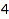 
with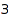 
nonnegative parts:
combinat::partitions::list(4, Length=3, MinPart=0)
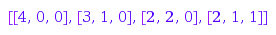
Two partitions are considered equivalent whenever they differ only by trailing zeroes. Whenever two equivalent partitions satisfy the constraints, only the shortest one is considered. Hence, this is the list of partitions of 
with at least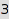 
nonnegative parts:
combinat::partitions::list(4, MinLength=3, MinPart=0)
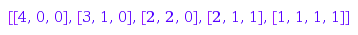
Example 4:
The options Inner, and Outer can be used to set part-by-part inclusion constraints. This is the list of the partitions of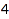 
with [3, 1, 1] as an outer bound:
combinat::partitions::list(4, Outer=[3, 1, 1])
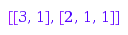
Outer sets MaxLength to the length of its argument. Moreover, the parts of Outer may be infinite to clear the constraint on specific parts. This is the list of the partitions of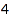 
of length at most 
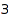such that that the second and third part are 
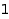when they exists:
combinat::partitions::list(4, Outer=[infinity, 1, 1])
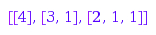
This is the list of the partitions of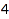 
with [1, 1, 1] as an inner bound:
combinat::partitions::list(4, Inner=[1, 1, 1])
Example 5:
The options MinSlope and MaxSlope can be used to set constraints on the slope, that is on the difference p[i+1]-p[i] of two consecutive parts. This is the list of the strictly decreasing partitions of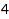 
:
combinat::partitions::list(4, MaxSlope=-1)
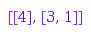
The default value for MaxSlope is zero to force the parts to be non-increasing. If MaxSlope is explicitly set to a positive number, the resulting lists are not necessarily partitions anymore since the parts may increase:
combinat::partitions::list(4, MaxSlope=1)
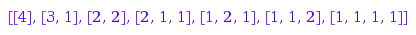
This is the list of the partitions of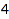 
such that the difference between two consecutive parts is at least 
:
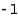combinat::partitions::list(4, MinSlope=-1)
This is the list of increasing partitions of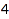 
:
combinat::partitions::list(4, MaxSlope=infinity, MinSlope=0)
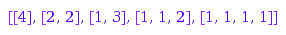
Example 6:
The constraints can be combined together in all reasonable ways. This is the list of the partitions of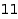 
of length between 
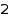and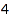 
such that the difference between two consecutive parts is between 
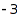and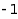 
:
combinat::partitions::list(11,
MaxSlope=-1, MinSlope=-3,
MinLength=2, MaxLength=4)
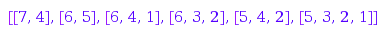
Idem with an Outer constraint:
combinat::partitions::list(11,
MaxSlope=-1, MinSlope=-3,
MinLength=2, MaxLength=4,
Outer=[6,5,2])
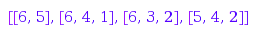
However, providing incoherent constraints may yield strange results. It is up to the user to ensure that the Inner and Outer partitions themselves satisfy the part and slope constraints:
combinat::partitions::list(5, Inner=[2, 1], MinPart=2)
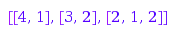
Example 7:
This is the conjugate of the partition [4, 1]:
combinat::partitions::conjugate([4, 1])
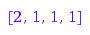
Geometrically, we just applied a reflection with respect to the main diagonal on the diagram of the partition. Of course, this operation is an involution:
combinat::partitions::conjugate([2, 1, 1, 1])
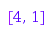
Example 8:
We describe how to generate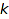 
-regular partitions. Recall that a partition p is 
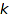-regular if no part is repeated more than 
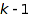times, or, equivalently, if the difference between any two consecutive parts of the conjugate partition pc is at most 
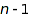. Here is a first (buggy) attempt to get the 
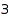-regular partitions of 
:
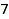map(combinat::partitions::list(7, MinSlope=-2),
combinat::partitions::conjugate)
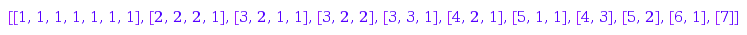
This is not quite correct: in [2,2,2,1], the first part is repeated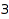 
times. Here is what happened: this 
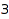is the last part of the conjugate partition [4,3], and we did not check the slope condition between this last part and the consecutive implicit zeroes. We ensure that the conjugate partition is padded with zeroes by setting Length=7+1. Note that combinat::partitions::conjugate allows partitions with padded zeroes. Now, here is the correct list of 
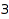regular partitions of 
:
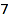map(combinat::partitions::list(7, MinSlope=-2, MinPart=0,
Length=7+1), combinat::partitions::conjugate)
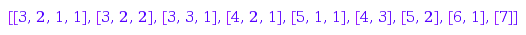
This trick is efficient, and can be refined further to generate regular partitions with length, part, or inclusion constraints.
Example 9:
This is the exponential notation of the partition [4, 1]:
combinat::partitions::toExp([6,4,4,2,1])
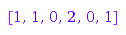
It can be converted back to the original partition:
combinat::partitions::fromExp([1, 1, 0, 2, 0, 1])
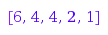
The exponential notation can be padded with extra zeroes:
combinat::partitions::toExp([6,4,4,2,1], 5);
combinat::partitions::toExp([6,4,4,2,1], 7);
combinat::partitions::toExp([6,4,4,2,1], 10);
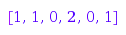
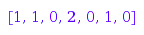
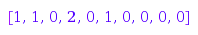
In any cases, converting back yields the original partition:
combinat::partitions::fromExp([1, 1, 0, 2, 0, 1, 0, 0, 0]);
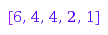
Example 10:
This example shows how to compute the corners of a partition.
combinat::partitions::corners([4, 3, 1])
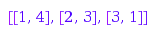
The corners can be represented graphically:
combinat::partitions::printPrettyCorners([4, 3, 1])
+---+
| * |
+---+---+---+
| | | * |
+---+---+---+---+
| | | | * |
+---+---+---+---+
Here is a more compact representation:
combinat::partitions::printCompactCorners([4, 3, 1])
*
##*
###*
Example 11:
Example of computation of a r-core and r-quotient of a partition:
combinat::partitions::rCore([6,3,2,2],3);
combinat::partitions::rQuotient([7,7,5,3,3,3,1],3)
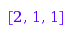
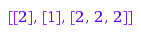
Rebuilding a partition from its r-core and its r-quotient:
combinat::partitions::fromCoreAndQuotient([2,1],[[2,1],[3],[1,1,1]]);
Example 12:
These are two example of adding and removing a vertical ribbon strip to a partition
combinat::partitions::addVerticalRibbonStrip([4, 3, 1], [2, 0, 0, 0, 2])
combinat::partitions::removeVerticalRibbonStrip([4, 3, 1], [0, 2, 0])
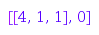
Example 13:
combinat::partitions::jacobiTrudy([4, 3, 1])
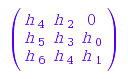
combinat::partitions::jacobiTrudy([4, 3, 1], T)
Background:
-
Partitions are naturally ordered lexicographically. The functions for counting and generating are directly inherited from Cat::IntegerListsLexClass with, by default, MaxSlope=0, and MinPart=1. The complexity of the generation algorithm is constant time amortized for each partition generated.
-
Without optional constraints, counting is done efficiently with Euler's pentagonal formula for small values of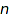 
and Hardy-Ramanujan-Rademacher's formula otherwise.
In all other cases, counting is done by brute force generation.
Changes in MuPAD 3.1
combinat::partitions(n) is now an alias for combinat::partitions::list(n), as in the other combinatorial classes.