muEC::SFA::SfAExpand – expands a SFA expression

expands a SFA expression

→ Examples

Call:

muEC::SFA::SfAExpand(sfa)

Parameters:

Related Functions:

muEC::SFA::SfACollect, muEC::SFA::SfAVars, muEC::SYMF::SfEval, muEC::SYMF::SfPlethysm

Details:

The muEC::SFA::SfAExpand function expands, whenever possible, any expression in SFA. It is a direct implementation of the -ring structure, i.e. symmetric functions are considered as operators over the ring of polynomials.

Expansion is inductively propagated, thus enabling chains of plethysms.

Alphabets are either formal alphabets (, , ...), or real constants (any float object or any formal variable which in not one of the , or variables (when explicitely so declared), or symmetric functions of SFA, or any linear combination of alphabets. For instance, 3/2*A1 + k*(A2 - s[3](-A1)) is a valid alphabet.

One may declare variables by setting e.g. SfAVars({{x}, {y}, z1, z2}). Here, z1, z2, all xi's, and all yi's will be held as variables within alphabets.

Rules used for e.g. power sums symmetric functions are:

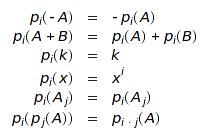
where is a real constant different of then , is an explicitely declared variable, is a formal alphabet and and are positive integers. Equivalent rules for the other bases are also implemented.

Example 1: