muEC::SFA::SfACollect – Collect and expand an symmetric function
collects products that are on algebraic bases (e, h, p) and expands products on linear bases (m, s)
→ Examples
Call:
muEC::SFA::SfACollect(sfa, <b | blist>)
Parameters:
|
sfa:
|
a linear combination of products of symmetric functions
|
|
b:
|
a basis
|
|
blist:
|
a list of bases
|
Related Functions:
muEC::SFA::SfAExpand, muEC::SFA::ToeA, muEC::SFA::TohA, muEC::SFA::TomA, muEC::SFA::TopA, muEC::SFA::TosA, muEC::SYMF::SfCollect
Details:
The muEC::SFA::SfACollect function transforms products of power sums, elementary and complete functions into a valid SFA expression.
Special algorithms are used for products of monomial symmetric functions and products of Schur functions.
The muEC::SFA::SfACollect function also normalizes indexing vectors of each symmetric function.
Valid bases are SFA::SFABases. They all are considered by default.
One may specify to collect products (and / or normalize indexing vectors) expressed only on specified bases by adding a second argument which is either a single basis or a list of bases.
Example 1:
muEC::SFA::SfACollect( p[3](A1)^4 * e[2](A2) * e[1](A2)
- q*s[2](A3)^2 );
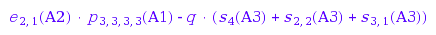
muEC::SFA::SfACollect( p[1,2](A1)^2 - q*m[1,0,0](A2)^2*s[1,3](A3)^2,
[ s, m ] );
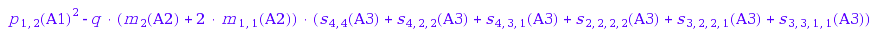
muEC::SFA::SfACollect( p[1,2](A1)^2 - q*m[1,0,0](A2)^2*s[1,3](A3)^2,
p ); // BROKEN EXAMPLE
2 2
p[2, 2, 1, 1](A1) - q s[1, 3](A3) m[1, 0, 0](A2)
![]()
![]()