combinat::integerListsLexTools – lexicographic generation of lists of integers
The library combinat::integerListsLexTools provides functions for the lexicographic generation of lists of integers under length, upper/lower bounds, and regularity constraints.
This is an internal library. It is used by the special purpose libraries combinat::partitions, combinat::compositions, and combinat::integerVectors which provide user-friendly interfaces.
This documentation is only provided here for the curious reader as well as for developers. The interface has been designed with efficiency in mind (no type checking, ...), and is subject to incompatible changes anytime in the future. Use at your own risk.
With the current algorithm, the constraints should satisfy the following conditions:
-
The upper and lower bounds themselves should satisfy the regularity constraints.
-
The maximal and minimal slopes values should not be equal.
-
The maximal and minimal part values should not be equal.
Those conditions are not checked by the algorithm, and the result may be completely incorrect if they are not satisfied.
→ Examples
Details:
-
Here, we call integer list a list l of nonnegative integers, its parts. By abuse, infinite parts will be allowed in some cases. The length of l is the number of its parts; the sum of l is the sum of its parts.
-
Let minSlope be an integer or 
and maxSlope be an integer or +infinity. Then an integer list is regular w.r.t. minSlope and maxSlope if minSlope <= l[i+1]-l[i] <= maxSlope, for all i. Regular functions are defined similarly.
-
Let f be a function, and l an integer list. Then, f is an upper bound (resp. lower bound) for l if l[i]<=f(i) (resp. f(i)<=l[i]) for all i.
-
A set of constraints is specified by a sequence of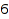 
objects minLength, maxLength, floor, ceiling, minSlope, maxSlope of the following types:
-
minLength: nonnegative integer;
-
maxLength: nonnegative integer or +infinity;
-
floor and ceiling: regular functions from [1..maxLength] to 0..+infinity;
-
minSlope: integer or -infinity;
-
maxSlope: integer or +infinity.
The purpose of this library is to generate all the valid integer lists of a given sum which satisfy all the specified constraints.
-
Two valid integer lists are considered equivalent if they only differ by trailing zeroes at positions. In this case, only the list with the least number of trailing zeroes will be generated.
Entries
|
"domtype"
|
The MuPAD domain used to represent integer lists: DOM_LIST
|
count – number of valid integer lists
combinat::integerListsLexTools::count(nonnegative integer n, constraints)
Returns the number of integer lists of sum n satisfying constraints.
generator – generator for valid integer lists
combinat::integerListsLexTools::generator(nonnegative integer n, constraints)
combinat::integerListsLexTools::generator(range range, constraints)
Returns a generator for the integer lists of sum n (resp. whose sum is in range) satisfying constraints.
The generator may return infinitely many elements. In case a range is provided, the results are returned by increasing sum; this is subject to change in a later release.
The range may be either of the form 2..7, or 1..infinity. In the later case, the generator may run into an infinite loop when there are only finitely many results if it does not manage to guess an upper bound on the sum.r
list – list of the valid integer lists
combinat::integerListsLexTools::list(nonnegative integer n, constraints)
Returns the list of the integer lists of sum n satisfying constraints.
first – first valid integer list
combinat::integerListsLexTools::first(nonnegative integer n, constraints)
Returns the first integer list of sum n satisfying constraints or FAIL if there is none.
Next – next valid integer list
combinat::integerListsLexTools::Next(integer list p, constraints)
Returns the integer list following p satisfying constraints or FAIL if there is none.
Example 1:
There are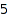 
partitions of 
:
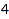combinat::integerListsLexTools::count(
4, 0, infinity, ()->0, ()->infinity, -infinity, 0)
Here is the list:
combinat::integerListsLexTools::list(
4, 0, infinity, ()->0, ()->infinity, -infinity, 0)
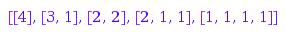
This is the list of all partitions of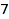 
with parts at least 
:
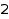combinat::integerListsLexTools::list(
7, 0, infinity, ()->2, ()->infinity, -infinity, 0)
This is the list of all partitions of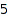 
which are bounded above by p:=[3,2,2]:
p:=[3,2,2]:
combinat::integerListsLexTools::list(
5, 0, nops(p), ()->0, i->p[i], -infinity, 0)
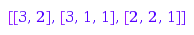
This is the list of all partitions of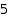 
which are bounded below by p:=[2,1,1]:
p:=[2,1,1]:
combinat::integerListsLexTools::list(
5, 0, nops(p), i->p[i], ()->+infinity, -infinity, 0)
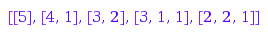
This is the list of all compositions of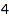 
:
combinat::integerListsLexTools::list(
4, 0, infinity, ()->1, ()->infinity, -infinity, infinity)
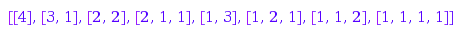
This is the list of all integer vectors of sum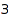 
and length 
:
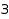combinat::integerListsLexTools::list(
3, 3, 3, ()->0, ()->infinity, -infinity, infinity)
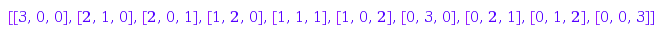
This is the list of all monomials of degree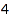 
which divide the monomial x^3y^1z^2 (a monomial being represented by its degree vector):
R:=Dom::DistributedPolynomial([x,y,z]):
m:=[3,1,2]:
map(combinat::integerListsLexTools::list(
4, nops(m), nops(m), ()->0, i->m[i], -infinity, infinity),
m1->R([[1,m1]]))
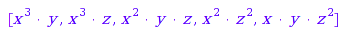
Example 2:
If maxLength=infinity and maxSlope>0, testing whether there exists a valid integer list of sum n may be only semi-decidable. In the following example, the algorithm will enter an infinite loop, because it needs to decide whether ceiling(i) is nonzero for some i:
combinat::integerListsLexTools::first(
1, 0, infinity, ()->0, ()->0, -infinity, infinity)
Background:
-
Except for one degenerate case where the algorithm may run forever without producing anything (see example 2), the complexity of the generation algorithm is constant time amortized for each integer list produced.
-
The generation algorithm could be extended to deal with non-constant slope constraints and with negative parts, as well as to accept a range parameter instead of a single integer for the sum n of the lists. Let us know if those would be useful features.
-
Counting is done by brute force generation.