combinat::compositions

combinat::compositions – compositions of an integer

The library combinat::compositions provides functions for counting, generating, and manipulating compositions.

→ Examples

Superdomain

Dom::BaseDomain

Categories

Cat::IntegerListsLexClass

Axioms

Ax::systemRep

Related Domains:

combinat::partitions, combinat::words

Details:

A composition c of a nonnegative integer n is a list of positive integers with total sum n.
All functions for counting and generating accept the following optional constraints on the compositions: MinLength, MaxLength, Length, MinPart, MaxPart, Inner, Outer, MinSlope, and MaxSlope. Cf. examples 3, 4, 5, 6, and 7.
Generally, compositions of 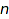are used to encode subsets of 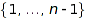through the bijection: 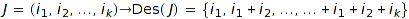. The set 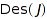is called the descents set of the composition 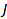. The converse bijection is given by

.

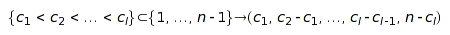In MuPAD the descents set can be stored as a set or as a list.
The inclusion of descents sets gives rise to a partial order on compositions:

.

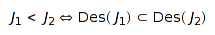This order is called the refinement order; the composition 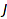is said to be finer than 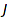, while 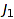is said to be fatter than 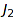. This order can be interpreted on compositions as follows: 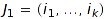is finer than 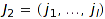if 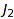can be obtained from 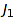by summing up together some consecutive parts of :

;

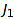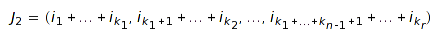the composition 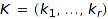is called the refinement composition of the pair .

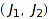Entries

"domtype"

The MuPAD domain of compositions: DOM_LIST

isA – test if an object is a composition

combinat::compositions::isA(any type co, <nonnegative integer n, <constraints>>)

Returns whether co is a composition.

If the optional argument n is present, returns whether co is a composition of n.

If constraints are given, returns whether co is a composition satisfying constraints.

count – number of compositions

combinat::compositions::count(nonnegative integer 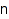, <constraints>)

Returns the number of compositions of n satisfying constraints.

generator – generator for compositions

combinat::compositions::generator(nonnegative integer 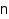, <constraints>)

Returns a generator for the compositions of n satisfying constraints.

list – list of the compositions

combinat::compositions::list(nonnegative integer 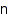, <constraints>)

Returns the list of the compositions of n satisfying constraints.

first – first composition

combinat::compositions::first(nonnegative integer 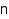, <constraints>)

Returns the first composition of n satisfying constraints or FAIL if there is none.

Next – next composition

combinat::compositions::Next(composition 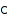, <constraints>)

Returns the composition following c satisfying constraints or FAIL if there is none.

descents – descents of a composition

combinat::compositions::descents(composition c)

Returns the list of descents of the composition c

descentsSet – descents of a composition

combinat::compositions::descentsSet(composition c)

Returns the set of descents of the composition c

fromDescents – composition of given descents

combinat::compositions::fromDescents(descent set s)

combinat::compositions::fromDescents(descent list l)

Returns the composition c whose descents set is s or l

majorIndex – major index of a composition

combinat::compositions::majorIndex(composition c)

Returns the major index composition c, defined as the sum of the descents.

isFiner – compare two compositions for the refinement order

combinat::compositions::isFiner(composition c1, composition c2)

Returns whether the composition c1 is finer than the composition c2.

finer – compositions finer than a composition

combinat::compositions::finer(composition c)

Returns the compositions finer than c. Note that compositons::finer is a full combinatorial class that implement the standard methods compositions::finer::count and compositions::finer::generators.

refinement – refinement compositions of a pair of compositions

combinat::compositions::refinement(composition c, composition d)

Returns the refinement compositions of the pair c,d. If c is not finer than d then returns FAIL.

fatter – compositions fatter than a composition

combinat::compositions::fatter(composition c)

Returns the compositions fatter than c. Note that compositons::fatter is a combinatorial class that implement the standard methods compositions::fatter::count and compositions::fatter::generators.

toSkewPartition – skew partition corresponding to a composition

combinat::compositions::toSkewPartition(composition 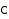, <nonnegative integer cover>)

Returns the skew partition corresponding to c. To a composition we can associate a skew partition where the length of the i-th line is the i-th part of the composition and the first cover cells are under the cells of the previous line. The default value for cover is 1.

Example 1:

This example shows how to test if an object is of type combinat::compositions:

combinat::compositions::isA([3,4]);

combinat::compositions::isA([3,4],7);

combinat::compositions::isA([3,4],5);

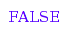
The combinat::compositions::isA function admets the same constraints than other functions in the package.

combinat::compositions::isA([4,2], 6, Inner=[2, 2], MinPart=2);

combinat::compositions::isA([4,2], 6, Inner=[2, 2], MaxPart=4);

Please note that given constraints should be compatible:

combinat::compositions::isA([4,1], 5, Inner=[2, 1], MinPart=2);

See further examples for other constraints.

Example 2:

There are 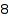compositions of :

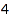combinat::compositions::count(4)

Here is the list:

combinat::compositions::list(4)

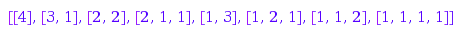
You can use the function combinat::compositions::first to get the “first” composition of a number:

combinat::compositions::first(4)

Using combinat::compositions::Next, you can calculate the “next” composition. This function takes as argument the composition relative to which you want the next one:

combinat::compositions::Next([4])

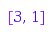
combinat::compositions::Next returns FAIL when the input is the last composition:

combinat::compositions::Next([1, 1, 1, 1])

When you want to run through the compositions of a number, you can generate them one by one to save memory:

g := combinat::compositions::generator(3):

g(); g(); g(); g(); g();

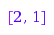
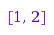
Typically, this would be used as follows:

g := combinat::compositions::generator(3):

while (p := g()) <> FAIL do print(p): end:

[3]

[2, 1]

[1, 2]

[1, 1, 1]

Example 3:

The options Length, MinLength, and MaxLength can be used to set length constraints. This is the list of the compositions of 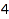of length :

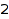combinat::compositions::list(4, Length=2)

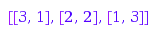
This is the list of the compositions of 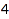of length at least :

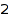combinat::compositions::list(4, MinLength=2)

This is the list of the compositions of 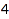of length at most :

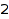combinat::compositions::list(4, MaxLength=2)

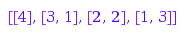
Setting both MinLength and MaxLength to the same value is equivalent to setting Length to this value. This is again the list of the compositions of 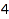of length :

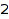combinat::compositions::list(4, MinLength=2, MaxLength=2)

Example 4:

The options MinPart and MaxPart can be used to set constraints on the sizes of all parts. Using MaxPart, you can select compositions having only small entries. This is the list of the compositions of 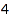with all parts at most :

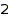combinat::compositions::list(4, MaxPart=2)

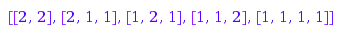
MinPart is complementary to MaxPart and selects compositions having only large parts (it takes a non-negative value). This is the list of the compositions of 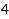with all parts at least :

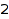combinat::compositions::list(4, MinPart=2)

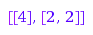
By default, the parts of a composition have to be positive. This can be changed using the option MinPart. In the following example, the options Length and MinPart are combined together to obtain the list of the compositions of 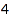with 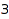nonnegative parts:

combinat::compositions::list(4, Length=3, MinPart=0)

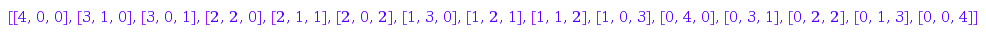
If the list you ask for is infinite, the program will not finish, as it is be the case for combinat::compositions::list(4, MinPart=0);

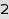Two compositions are considered equivalent whenever they differ only by trailing zeroes. Whenever two equivalent compositions satisfy the constraints, only the shortest one is considered. Hence, this is the list of compositions of with or 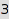nonnegative parts:

combinat::compositions::list(4, MinLength=2, MaxLength=3, MinPart=0)

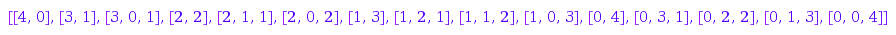
Example 5:

The options Inner, and Outer can be used to set part-by-part containment constraints. This is the list of the compositions of 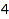bounded above by [3, 1, 2]:

combinat::compositions::list(4, Outer=[3, 1, 2])

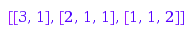
Outer sets MaxLength to the length of its argument. Moreover, the parts of Outer may be infinite to clear the constraint on specific parts. This is the list of compositions of 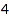of length at most 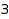such that the first and third parts are at most :

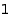combinat::compositions::list(4, Outer=[1, infinity, 1])

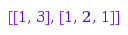
This is the list of compositions of 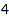bounded below by [1, 1, 1]:

combinat::compositions::list(4, Inner=[1, 1, 1])

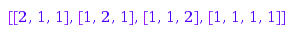
Example 6:

The options MinSlope and MaxSlope can be used to set constraints on the slope, that is on the difference p[i+1]-p[i] of two consecutive parts. This is the list of the increasing compositions of :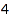

combinat::compositions::list(4, MinSlope=0)

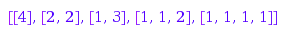
This is the list of compositions of 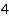such that two consecutive parts differ by at most one unit:

combinat::compositions::list(4, MinSlope=-1, MaxSlope=1)

Example 7:

The constraints can be combined together in all reasonable ways. This is the list of compositions of 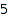of length between 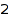and 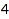such that the difference between two consecutive parts is between 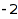and :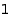

combinat::compositions::list(5,

MaxSlope=1, MinSlope=-2,

MinLength=2, MaxLength=4)

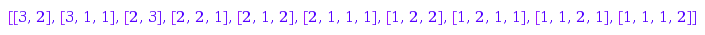
Idem with an Outer constraint:

combinat::compositions::list(5,

MaxSlope=1, MinSlope=-2,

MinLength=2, MaxLength=4,

Outer=[2,5,2])

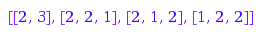
However, providing incoherent constraints may yield strange results. It is up to the user to ensure that the Inner and Outer compositions themselves satisfy the parts and slope constraints:

combinat::compositions::list(5, Inner=[2, 1], MinPart=2)

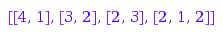
Example 8:

One can check that those two compositions are not comparable for the refinement order:

combinat::compositions::isFiner([4,1,2],[3,1,3]);

combinat::compositions::isFiner([3,1,3],[4,1,2])

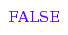
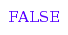
To get the list of compositions finer than [4,1,2], you can use:

combinat::compositions::finer::list([4,1,2]);

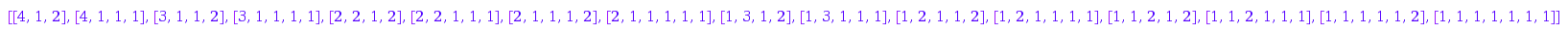
The composition [1, 2, 2, 1, 1, 2] is finer than the composition [5,1,3]:

combinat::compositions::isFiner([1, 2, 2, 1, 1, 2], [5, 1, 3])

The reason is that [1, 2, 2] is a composition of 5, [1] is a composition of 1 and [1, 2] is a composition of 3. The lengths [3, 1, 2] of [1, 2, 2], [1], [1, 2] is the refinement composition and is computed by MuPAD by the command:

combinat::compositions::isFiner([1, 2, 3, 1, 2], [5, 1, 3]);

combinat::compositions::refinement([1, 2, 2, 1, 1, 2], [5, 1, 3])

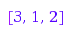
To get the list of compositions fatter than [4,1,2], you can use:

combinat::compositions::fatter::list([4,1,2]);

If you only want their number, you can ask:

combinat::compositions::fatter::count([4,1,2]);

Example 9:

Conversion from compositions to skew partitions with two values for the covering parameter.

combinat::skewPartitions::printPretty(combinat::compositions::toSkewPartition([3, 4, 1]))

+---+---+---+

| | | |

+---+---+---+---+---+---+

| | | | |

+---+---+---+---+

| |

+---+

combinat::skewPartitions::printPretty(combinat::compositions::toSkewPartition([3, 4, 1], 0))

+---+---+---+

| | | |

+---+---+---+---+---+---+---+

| | | | |

+---+---+---+---+---+

| |

+---+

An equivalent way to have the same output is to call combinat::compositions::printPretty with the composition and the optional covering paramater.

Background:

Compositions are naturally ordered lexicographically. The functions for counting and generating are directly inherited from Cat::IntegerListsLexClass with, by default, MinPart=1. The complexity of the generation algorithm is constant time amortized for each composition generated.
Except for the trivial cases, counting is done by brute force generation.