combinat::dyckWords – Dyck words
The library combinat::dyckWords provides functions for counting, generating, and manipulating Dyck words.
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::DecomposableClass
Axioms
Ax::systemRep
Related Domains:
combinat::binaryTrees, combinat::nonCrossingPartitions
Details:
-
A Dyck word of size n is a word with n ones and n zeroes such that in any prefix there are more ones than zeroes.
-
A Dyck word can be interpreted as a word of well balanced parenthesis by substituting ones with opening parenthesis and zeroes with closing parenthesis.
-
A prefix Dyck word is a non completed Dyck word, that is, a word with more opening parenthesis than closing parenthesis.
-
Geometrically, a Dyck word is also a discrete path in the nonnegative plane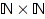 
, going from 
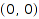to 
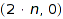, with right-up steps (ones) and right-down steps (zeroes).
-
Dyck words of length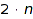 
are in bijection with many other discrete classes like rooted ordered trees on 
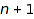nodes, binary trees on 
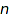nodes, complete binary trees on 
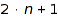nodes, 
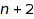-gone triangulations, standard tableaux with 
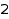lines of width 
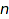or 
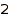columns of height 
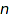, non crossing set partitions of 
, etc. They are counted by the Catalan numbers.
Entries
|
"domtype"
|
The MuPAD domain of Dyck words: DOM_LIST
|
|
"typePrefix"
|
The MuPAD type of prefix Dyck words.
|
isA – test if an object is a Dyck word
combinat::dyckWords::isA(any type dw, <nonnegative integer n1, nonnegative integer n2>)
Returns whether the object dw is a Dyck word.
If the optional argument is present, returns whether dw is a a Dyck word of length 2n1.
If the two optional arguments are present, returns whether dw is a (prefix) Dyck word of n1 opening parenthesis and n2 closing parenthesis.
isAPrefix – test if an object is a prefix Dyck word
combinat::dyckWords::isAPrefix(any type dw, <nonnegative integer n1, nonnegative integer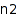 
>)
Returns whether the object dw is a prefix Dyck word.
If the optional arguments are present, returns whether dw is a prefix Dyck word of n1 opening parenthesis and n2 closing parenthesis.
count – number of Dyck words
combinat::dyckWords::count(nonnegative integer n)
Returns the number of Dyck words of size n, i.e. the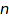 
-th Catalan number.
generator – generator for Dyck words
combinat::dyckWords::generator(nonnegative integer n)
Returns a generator for Dyck words of size n.
list – list of Dyck words
combinat::dyckWords::list(nonnegative integer n)
combinat::dyckWords::list(nonnegative integer n1, nonnegative integer n2)
Returns the list of Dyck words of size n.
Returns the list of prefix Dyck words, with n1 ones and n2 zeroes.
toString – conversion to string of well balanced parenthesis
combinat::dyckWords::toString(Dyck word w)
Returns the string of well balanced parenthesis corresponding to the Dyck word w, replacing "1" with "(" and "0" with ")". Note that the function works even if the word is not well balanced.
See also the function combinat::dyckWords::fromString
fromString – conversion from string of well balanced parenthesis
combinat::dyckWords::fromString(string s)
Returns the Dyck word corresponding to the string of well balanced parenthesis s, replacing "(" with "1" and ")" with "0". Note that the function does not check if the string is indeed well balanced.
See also combinat::dyckWords::toString
printPretty – print a Dyck word as a Dyck path
combinat::dyckWords::printPretty(Dyck word w)
Returns a output::asciiArt which prints out as a Dyck path. A Dyck path is a path in the integer quarter of plane starting from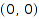 
using only north-est and south-east step and ending on the 
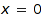axis. The conversion is done as follows: the "1"s correspond to north-est step whereas the "0"s corresponds to south-east step.
toNonCrossingPartition – Biane bijection to non crossing set partitions
combinat::dyckWords::toNonCrossingPartition(Dyck word w)
Returns the non-crossing set partition corresponding to the Dyck word w by the Biane bijection.
See also combinat::nonCrossingPartitions and combinat::dyckWords::fromNonCrossingPartition
Reference: Philippe Biane, Permutations suivant le type d'excédances et le nombre d'inversions et interprétation combinatoire d'une fraction continue de Heine, Europ. J. Comb., 14(4): 277-284, 1993
fromNonCrossingPartition – Biane bijection from non-crossing set partitions
combinat::dyckWords::fromNonCrossingPartition(non crossing set partition p)
Returns the Dyck word corresponding to the non crossing set partition p by the Biane bijection.
See also combinat::dyckWords::toNonCrossingPartition
fromOrderedTree – canonical bijection from ordered trees to Dyck words
combinat::dyckWords::fromOrderedTree(ordered tree t)
Returns the Dyck word corresponding to the ordered tree t.
This implements the canonical bijection from ordered trees with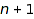 
nodes to Dyck words of size 
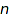such that if a tree 
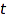has 
as childs then 
.
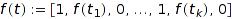See also combinat::trees and combinat::dyckWords::toOrderedTree.
toOrderedTree – canonical bijection from Dyck words to ordered trees
combinat::dyckWords::toOrderedTree(Dyck word w)
Returns the ordered tree corresponding to the Dyck word w.
See also combinat::dyckWords::fromOrderedTree.
toBinaryTree – bijection from Dyck words to binary trees
combinat::dyckWords::toBinaryTree(Dyck word w)
Returns the binary tree corresponding to the Dyck word w.
See also combinat::binaryTrees and combinat::dyckWords::fromBinaryTree
We use the standard bijection associated to the factorization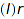 
where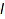 
and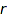 
are Dyck words : 
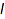and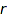 
corresponds to the left and right subtrees.
fromBinaryTree – bijection from binary trees to Dyck words
combinat::dyckWords::fromBinaryTree(binary trees t)
Returns the Dyck word corresponding to the binary trees t.
See also combinat::dyckWords::toBinaryTree
Example 1:
There are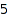 
Dyck words of size 
:
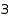combinat::dyckWords::count(3)
Here is the list:
combinat::dyckWords::list(3)
They correspond to the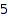 
strings of well-balanced parenthesis of length 
:
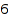map(combinat::dyckWords::list(3), combinat::dyckWords::toString)
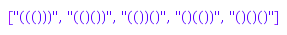
On the other hand, neither [1,0,0,1,1,0] nor [1,1,1,1,0,0] are Dyck words:
combinat::dyckWords::toString([1,0,0,1,1,0]);
combinat::dyckWords::toString([1,1,1,1,0,0])
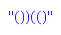
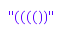
Example 2:
In this example we check the type of some Dyck words.
combinat::dyckWords::isA([1, 1, 1, 0, 0, 0]);
combinat::dyckWords::isA([1, 1, 1, 0, 0, 0], 3);
combinat::dyckWords::isA([1, 1, 1, 0, 0, 0], 2);
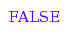
The list [1,0,0,1,1,0] is not a Dyck word:
combinat::dyckWords::isA([1, 0, 0, 1, 1, 0]);
combinat::dyckWords::isA([1, 0, 0, 1, 1, 0], 3);
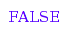
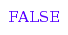
The list [1,1,1,1,0,0] is not a Dyck word, but a prefix Dyck word:
combinat::dyckWords::isA([1, 1, 1, 1, 0, 0]);
combinat::dyckWords::isA([1, 1, 1, 1, 0, 0], 4, 2);
combinat::dyckWords::isAPrefix([1, 1, 1, 1, 0, 0]);
combinat::dyckWords::isAPrefix([1, 1, 1, 1, 0, 0], 4, 2);
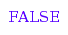
Example 3:
One can convert a Dyck word to a string of well-balanced parenthesis:
combinat::dyckWords::toString([1,1,1,0,1,1,0,0,0,1,0,0,1,1,1,0,0,0,1,0]);
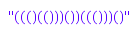
And convert it back:
combinat::dyckWords::fromString("((()(()))())((()))()");
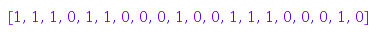
Example 4:
One can print a Dyck word as a Dyck path:
combinat::dyckWords::printPretty([1,1,1,0,1,1,0,0,0,1,0,0,1,1,1,0,0,0,1,0]);
/\
/\/ \ /\
/ \/\ / \
/ \/ \/\
The return value is a MuPAD object which belongs to the domain output::asciiArt
domtype(combinat::dyckWords::printPretty([1,1,1,0,1,1,0,0,0,1,0,0,1,1,1,0,0,0,1,0]));
Example 5:
Dyck words of size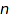 
are in bijection with non-crossing set partitions of 
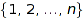. Here is the the image of [1,0,1,0,1,0] by the Biane bijection:
combinat::dyckWords::toNonCrossingPartition([1,0,1,1,0,0,1,0])
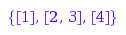
We can reconstruct the original Dyck word:
combinat::dyckWords::fromNonCrossingPartition({[1], [4], [2, 3]})
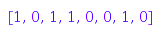
Here is the list of all non-crossing set partitions of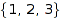 
:
map(combinat::dyckWords::list(3),
combinat::dyckWords::toNonCrossingPartition)
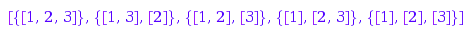
Example 6:
Dyck words of size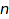 
are in bijection with binary trees. Here is the the image of [1,0,1,0,1,0]:
t := combinat::dyckWords::toBinaryTree([1, 0, 1, 1, 0, 0, 1, 0])
o
\
/\
We can reconstruct the original Dyck word:
combinat::dyckWords::fromBinaryTree(t)
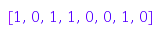
Here is the list of all binary trees of size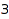 
:
map(combinat::dyckWords::list(4),
combinat::dyckWords::toBinaryTree)
-- o, o, o, o , o, o, o , o , o , o , o , o , o , o --
| / / / / \ / / / \ / \ / \ \ \ \ \ \ |
| / / /\ / \ \ \ / \ / / /\ \ \ |
-- / \ / \ / \ / \ --
Note that the order is not the same as the order chosen on binary trees, which is more symmetric.
combinat::binaryTrees::list(4)
-- o , o , o , o , o , o , o , o , o , o, o, o, o, o --
| \ \ \ \ \ / \ / \ / \ / \ / / / / / |
| \ \ /\ / / \ / \ / \ \ /\ / / |
-- \ / \ / \ / \ / --
Background:
Dyck words are naturally ordered lexicographically.