combinat::nonCrossingPartitions – non crossing set partitions
The library combinat::nonCrossingPartitions provides functions for non crossing set partitions.
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass
Axioms
Ax::systemRep
Details:
-
A non crossing set partition of 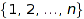 is a partition
is a partition 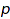 of the set
of the set 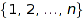 such that there is no
such that there is no 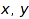 in one part of
in one part of 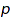 and
and 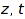 in another part of
in another part of 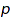 with
with 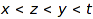 . For example, [1,3,7], [2], [4,5], [6], [8,9] is a non crossing set partition, but [1,3], [2,4] is not (take x=1, y=3, z=2, t=4).
. For example, [1,3,7], [2], [4,5], [6], [8,9] is a non crossing set partition, but [1,3], [2,4] is not (take x=1, y=3, z=2, t=4).
-
A non crossing set partition of 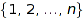 is represented as a set of lists. Each list represents a part of the partition, with its elements in increasing order.
is represented as a set of lists. Each list represents a part of the partition, with its elements in increasing order.
-
Non crossing set partitions are in bijection with Dyck words (library combinat::dyckWords), and many other discrete classes.
Entries
|
"domtype"
|
The MuPAD domain used to represent non crossing set partitions: DOM_SET
|
count – number of non crossing set partitions
combinat::nonCrossingPartitions::count(nonnegative integer n)
Returns the number of non crossing set partitions of size n.
generator – generator for non crossing set partitions
combinat::nonCrossingPartitions::generator(nonnegative integer n)
Returns a generator for the non crossing set partitions of size n.
list – list of the non crossing set partitions
combinat::nonCrossingPartitions::list(nonnegative integer n)
Returns the list of the non crossing set partitions of size n.
Example 1:
There are 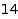 non crossing set partitions of size
non crossing set partitions of size 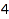 :
:
combinat::nonCrossingPartitions::count(4)

Here is the list:
combinat::nonCrossingPartitions::list(4)
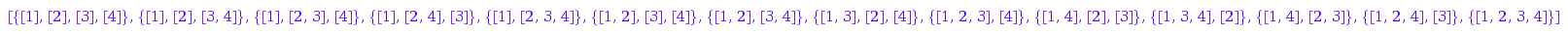
To generate non crossing set partitions of a given size:
g:= combinat::nonCrossingPartitions::generator(3):
g(); g(); g(); g(); g(); g()
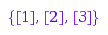
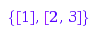
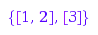
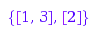
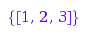

Typically, this would be used as follows:
g := combinat::nonCrossingPartitions::generator(3):
while (p := g()) <> FAIL do print(p): end:
{[1], [2], [3]}
{[1], [2, 3]}
{[1, 2], [3]}
{[1, 3], [2]}
{[1, 2, 3]}
Example 2:
Non crossing set partitions implements the Biane bijection with Dyck words.
combinat::dyckWords::count(i) $ i = 1..6;
combinat::nonCrossingPartitions::count(i) $ i = 1..6
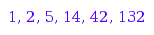
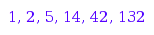
And here is a little list comparation:
map(combinat::dyckWords::list(3),
combinat::dyckWords::toNonCrossingPartition);
combinat::nonCrossingPartitions::list(3)
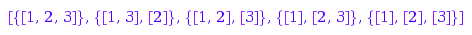
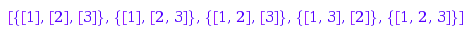
![]() is a partition
is a partition ![]() of the set
of the set ![]() such that there is no
such that there is no ![]() in one part of
in one part of ![]() and
and ![]() in another part of
in another part of ![]() with
with ![]() . For example, [1,3,7], [2], [4,5], [6], [8,9] is a non crossing set partition, but [1,3], [2,4] is not (take x=1, y=3, z=2, t=4).
. For example, [1,3,7], [2], [4,5], [6], [8,9] is a non crossing set partition, but [1,3], [2,4] is not (take x=1, y=3, z=2, t=4).![]() is represented as a set of lists. Each list represents a part of the partition, with its elements in increasing order.
is represented as a set of lists. Each list represents a part of the partition, with its elements in increasing order.