combinat::binaryTrees – binary trees
The library combinat::binaryTrees provides functions for counting, generating, and manipulating binary trees.
→ Examples
Creating Elements
combinat::binaryTrees(list)
Parameters:
|
list:
|
A nested list of lists.
|
Superdomain
combinat::trees
Categories
Cat::DecomposableClass, Cat::CombinatorialClass
Axioms
Ax::normalRep, Ax::canonicalRep
Related Domains:
combinat::decomposableObjects, combinat::dyckWords, combinat::labelledBinaryTrees, combinat::trees
Details:
-
A binary tree is either empty, or constructed recursively from two trees by attaching them to a common ancestor node. Technically, it is a combinat::trees such that every node exactly has two operands: the left and the right subtree.
-
A complete binary tree is a binary tree where each interior node (not a leaf) has non-empty left and right subtrees.
-
The binary trees of size 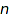 are enumerated by the Catalan numbers. So they are in bijection with Dyck words.
are enumerated by the Catalan numbers. So they are in bijection with Dyck words.
Details:
combinat::binaryTrees(list) creates a new binary tree whose recursive structure is encoded by list. See combinat::trees for details on the structure of the list.
Entries
|
"zero"
|
The empty binary tree with zero nodes
|
|
"one"
|
The binary tree with one single node with two empty subtrees
|
|
"dummyLabel"
|
The dummy label which is used for unlabelled binary trees
|
Method size is inherited from combinat::trees.
Method nops is inherited from combinat::trees.
Method op is inherited from combinat::trees.
Method subsop is inherited from combinat::trees.
Method _index is inherited from combinat::trees.
Method set_index is inherited from combinat::trees.
Method expr is inherited from combinat::trees.
Method print is inherited from combinat::trees.
isA – test if an object is a binary tree
combinat::binaryTrees::isA(any type bt, <nonnegative integer n>)
Returns whether the object bt is a binary tree.
If the optional argument is present, returns whether bt is a a binary tree of size n.
count – number of binary trees
combinat::binaryTrees::count(nonnegative integer n)
Returns the number of binary trees of size n.
generator – generator for binary trees
combinat::binaryTrees::generator(nonnegative integer n)
Returns a generator for the binary trees of size n.
list – list of the binary trees
combinat::binaryTrees::list(nonnegative integer n)
Returns the list of the binary trees of size n.
unrank – unranking of a binary tree
combinat::binaryTrees::unrank(nonnegative integer n, nonnegative integer i)
Returns the i-th binary tree of size n.
random – random tree
combinat::binaryTrees::random(nonnegative integer n)
Returns a random binary tree of size n.
Method revert is inherited from combinat::trees.
branchSlice – left or right branch slice of a binary tree
combinat::binaryTrees::branchSlice(binary tree t, <direction>)
direction can be Left or Right. Returns the list of the binary trees without left (resp. right) subtrees obtained by slicing the left (resp. right) branch of t, ordered from top to bottom.
toDyckWord – Transformation of a tree into a Dyck word
combinat::binaryTrees::toDyckWord(binary tree t)
Returns the Dyck word corresponding to the tree.
fromDyckWord – Transformation of a Dyck word into a tree
combinat::binaryTrees::fromDyckWord(dyck word w)
Returns the tree corresponding to the Dyck word.
shuffle – shuffle product of two binary trees
combinat::binaryTrees::shuffle(binary tree t1, binary tree t2)
Returns the shuffle product of t1 and t2.
Example 1:
We first define an alias for dummy labels (see combinat::trees for explanations on this):
alias(d = combinat::trees::dummyLabel):
We introduce here a binary tree of size 5, and test its type:
bt:=combinat::binaryTrees([d, [d, [d, [d, [], []], []],
[d, [], []]], []]);
combinat::binaryTrees::isA(bt);
combinat::binaryTrees::isA(bt,5);
combinat::binaryTrees::isA(bt, 3);
o
/
/\
/


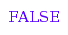
There is a strong difference between the binary tree and the list used in its construction:
combinat::binaryTrees::isA([d, [d, [d, [d, [], []], []],
[d, [], []]], []]);
domtype([d, [d, [d, [d, [], []], []], [d, [], []]], []]);
domtype(bt);
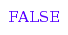
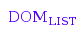

Example 2:
There are 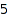 trees of size
trees of size 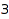 :
:
combinat::binaryTrees::count(10);
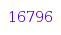
If you want to run through the trees of size 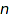 , you can generate them one by one to save memory:
, you can generate them one by one to save memory:
g := combinat::binaryTrees::generator(3):
g();
g(), g(), g(), g(), g();
o
\
\
o , o , o, o, FAIL
\ / \ / /
/ \ /
Example 3:
In this example, we list all the trees on 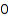 to
to 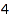 nodes:
nodes:
for i from 0 to 4 do
print(combinat::binaryTrees::list(i))
end_for
[.]
[o]
o , o
[ \ / ]
-- o , o , o , o, o --
| \ \ / \ / / |
-- \ / \ / --
-- o , o , o , o , o , o , o , o , o , o, o, o, o, o --
| \ \ \ \ \ / \ / \ / \ / \ / / / / / |
| \ \ /\ / / \ / \ / \ \ /\ / / |
-- \ / \ / \ / \ / --
We can directly get the sixth tree of size 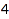 :
:
combinat::binaryTrees::unrank(6,4);
o
/ \
\
We can select a random binary tree by:
combinat::binaryTrees::random(10);
o
/ \
/\ /\
/
\
\
We define a binary tree by hand:
t := combinat::binaryTrees([d, [d, [d, [], [d]], []], [d, [d]]])
o
/ \
/ /
\
The tree can be converted back into a list of lists. Note that the constructor added automatically the missing empty lists:
expr(t)

We can slice the left or the right branch of t:
combinat::binaryTrees::branchSlice(t, Left)
-- o , o, o --
| \ \ |
-- / --
combinat::binaryTrees::branchSlice(t, Right)
-- o, o --
| / / |
| / |
-- \ --
Example 4:
Let us start with a binary tree:
combinat::binaryTrees::unrank(12,7);
o
\
\
\
/
/\
We can compute its image under the usual bijection with Dyck words:
combinat::binaryTrees::toDyckWord(
combinat::binaryTrees::unrank(12,7));
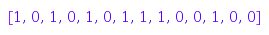
![]() are enumerated by the Catalan numbers. So they are in bijection with Dyck words.
are enumerated by the Catalan numbers. So they are in bijection with Dyck words.