combinat::decomposableObjects – decomposable combinatorial objects
The library combinat::decomposableObjects(specification) provides functions for counting, generating, and drawing at random the decomposable combinatorial objects defined recursively by specification.
→ Examples
Creating the Type
combinat::decomposableObjects(specification, <Options>)
Parameters:
|
specification:
|
A combinatorial specification
|
Options:
|
Labelled = 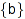 : :
|
Selects between labeled or unlabeled combinatorial objects. b must be TRUE or FALSE. The default value is FALSE.
|
|
Products = 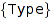 : :
|
Choose the counting algorithm. Type is one of Naive, Holonomic. The default value is Holonomic for context free grammars, and Naive otherwise. See "count" for details.
|
|
MainNonTerminal = 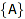 : :
|
Specifies the main non terminal of the specification. A must be a non terminal appearing in the specification. By default, the first one (as returned by op(specification,[1,1]) is used). This option used to be incorrectly named MainTerminal.
|
|
Boustrophedonic = 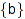 : :
|
Specifies the order in which elements of products are generated; see “background” section for more details. b must be TRUE or FALSE. The default value is TRUE.
|
|
Float = 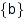 : :
|
Specifies whether floating point arithmetic should be used for fast approximate counting; see the example 8 for details. b must be TRUE or FALSE. The default value is FALSE.
|
Details:
-
A decomposable combinatorial class is recursively built from basic classes using constructors. The basic classes are:
-
Epsilon or Epsilon(A):a class containing a single object of size zero, named Epsilon or A; as a syntactic sugar, a production of the form A = Epsilon is rewritten into A = Epsilon(A);
-
Atom or Atom(A):a class containing a single object of size one, named Atom or A; as a syntactic sugar, a production of the form A = Atom is rewritten into A = Atom(A); one can also specify weights for atoms and epsilons; see the example 8 for details;
-
Z:this is equivalent to Atom(Z), and is provided as a syntactic sugar;
-
Predefined(countrandomunrank):a class described by the functions count, random, unrank;
-
Domain(class) or class: a combinatorial class represented by the MuPAD domain class (see Cat::CombinatorialClass).
The available constructors are:
-
Union(A, B, ...): the disjoint union of the classes A, B, ...
-
Prod(A, B, ...): the partitional product of the classes A, B, ...
-
BoxedProd(A, B, ...): (for labelled structures) similar to Prod, but forces the smallest label to be on the A side.
-
Sequence(A): all sequences of elements of A; A should not contain elements of size zero
-
Multiset(A): all sets of elements of A with repetitions; A should not contain elements of size zero
-
Powerset(A): all sets of elements of A without repetitions; A should not contain elements of size zero
-
Cycle(A): all directed cycles of elements of A, including the empty cycle; A should not contain elements of size zero
-
Alias(A), Alias(A,f): an alias to the class A, or the image of the class A by the function f.
The constructor Sequence as well as, in the labelled case, the constructors Powerset, Multiset, and Cycle accept further options MinLength, MaxLength, and Length to set length restrictions: for example, Sequence(A, MinLength=3, MaxLength=5) represents all the sequences of elements of A of length between 3 and 5.
-
A combinatorial specification is a list (or set or table) of productions of the form A = <rhs>, where A is the name of the class being defined, and <rhs> is an expression involving elementary classes, constructors and other classes. A is called a non terminal. For example, below are the specifications of some well-known combinatorial classes:
Labelling type = 'labelled':
|
[A = Prod(Z,Powerset(A))]
|
non plane trees
|
|
[B = Union(Z,Prod(B,B))]
|
plane binary trees
|
|
[C = Prod(Z,Sequence(C))]
|
plane general trees
|
|
[D = Powerset(Cycle(Z))]
|
permutations in cycle notation
|
|
[E = Powerset(Cycle(A)), A=Prod(Z,Powerset(A))]
|
functional graphs
|
|
[F = Powerset(Powerset(Z,MinLength=1))]
|
set partitions
|
|
[G = Union(Z,Prod(Z,Powerset(G,Length=3)))]
|
non plane ternary trees
|
|
[H = Union(Z,Powerset(H,MinLength=2))]
|
hierarchies
|
|
[L = Powerset(Powerset(Powerset(Z,MinLength=1),MinLength=1))]
|
3-balanced hierarchies
|
|
[M = Sequence(Powerset(Z,MinLength=1))]
|
surjections
|
|
[A = Multiset(Sequence(Z,MinLength=1))]
|
integer partitions
|
|
[B = Sequence(Union(Z,Z))]
|
binary sequences
|
|
[C = Cycle(Sequence(Z,MinLength=1))]
|
necklaces
|
|
[D = Prod(Z,Multiset(D))]
|
rooted unlabelled trees
|
|
[E = Powerset(Cycle(D)), D=Prod(Z,Powerset(D))]
|
random mappings patterns
|
|
[F = Union(Z,Multiset(F,Length=2))]
|
nonplane binary trees
|
|
[G = Union(Z,Multiset(G,Length=3))]
|
nonplane ternary trees
|
|
[H = Union(Z,Multiset(H,MinLength=2))]
|
unlabelled hierarchies
|
-
Note: some of the unlabelled specifications above require not yet implemented features.
-
A specification is context free if it only uses the constructors Prod and Union, and those derived from them like Sequence. In particular this excludes the Powerset, Multiset, and Cycle constructions. Some features of this library are only available for context free specifications.
-
When the specification uses Domain(class), the system can of course only do counting if the provided domain class can, and similar wise for random, unrank, ...
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass
Axioms
Ax::systemRep
count – number of decomposable objects
(combinat::decomposableObjects(specification, <Options>))::count(nonnegative integer n, <A>)
Returns the number of objects of size n derived by the non terminal A in the specification.
By default, A is the main non terminal.
If Products is set to Naive, the counting is done by naive products of generating series; this gives a 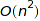 complexity (not counting the coefficient growth). Those products could be done using a lazy Karatsuba-type algorithm with a complexity of O(n^3/2); however this is currently only partly implemented (Products will be Lazy).
complexity (not counting the coefficient growth). Those products could be done using a lazy Karatsuba-type algorithm with a complexity of O(n^3/2); however this is currently only partly implemented (Products will be Lazy).
If Products is set to Holonomic, the system will first precompute a linear recurrence between the coefficients of the generating series (see "recurrenceRelation"), and then use it for the counting; this gives a complexity of 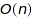 . This is only possible for context free specifications. Also, for very large specifications (say more than 100 non terminals), the precomputation can become quite expensive; if one is only interested in counting for small values of
. This is only possible for context free specifications. Also, for very large specifications (say more than 100 non terminals), the precomputation can become quite expensive; if one is only interested in counting for small values of 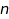 (say
(say 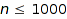 ), it may be preferable to stick to Naive or Lazy products.
), it may be preferable to stick to Naive or Lazy products.
generator – generator for decomposable objects
(combinat::decomposableObjects(specification, <Options>))::generator(nonnegative integer n, <A>)
Returns a generator for the objects of size n derived by the non terminal A in the specification.
By default, A is the main non terminal.
list – list of decomposable objects
(combinat::decomposableObjects(specification, <Options>))::list(nonnegative integer n, <A>)
Returns the list of the objects of size n derived by the non terminal A in the specification.
By default, A is the main non terminal.
Currently, this method is based on "unrank", and only works for context free grammars.
unrank – unranking of decomposable objects
(combinat::decomposableObjects(specification, <Options>))::unrank(nonnegative integer i, nonnegative integer n, <A>)
Returns the i-th object of size n derived by the non terminal A in the specification.
By default, A is the main non terminal.
Currently, this method only works for context free grammars; algorithm do exists for the other constructions, but are not yet implemented.
The worst case complexity is 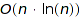 with the Boustrophedonic order, and
with the Boustrophedonic order, and 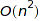 otherwise.
otherwise.
random – random object
(combinat::decomposableObjects(specification, <Options>))::random(nonnegative integer n, <A>)
Returns a random object of size n derived by the non terminal A in the specification.
By default, A is the main non terminal.
The worst case complexity is 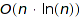 with the Boustrophedonic order, and
with the Boustrophedonic order, and 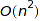 otherwise.
otherwise.
standardSpecification – specification in standard form
(combinat::decomposableObjects(specification, <Options>))::standardSpecification()
Returns the standard form of the specification; this is an equivalent specification which uses only the constructors Atom, Union, Prod, Theta, Int, Delta, DivX, and MultX. Theta is the pointing constructor, Int the formal inverse of Theta, and Delta is the generalized diagonal.
standardSpecificationCount – specification in standard form
(combinat::decomposableObjects(specification, <Options>))::standardSpecificationCount()
Returns a simplified form of the specification in standard form which is equivalent for counting purposes.
This is done by sorting the operands of Prod and Union (the operations + and * on generating series are commutative!), erasing the names of the singletons and atoms and assigning them with a default weight if they do not have one yet. Then, the productions that are identical are factored out using Alias. Further optimizations would be possible; in particular, productions that are recursively equivalent are not detected yet.
algebraicEquation – algebraic equation for the generating series
(combinat::decomposableObjects(specification, <Options>))::algebraicEquation(<{A}>)
Returns an algebraic equation satisfied by the generating series for the non terminal A.
Computing this algebraic equation is only possible if the specification is context free; FAIL is returned if this is not the case.
recurrenceRelation – recurrence relation for the coefficients of the generating series
(combinat::decomposableObjects(specification, <Options>))::recurrenceRelation(<{A}>, <identifier u>, <identifier u>)
Returns a recurrence relation between the coefficients of the generating series for the non terminal A.
The recurrence relation is given in the form of an expression such as u(n) - n*u(n-1) - u(n-2), it means that the number of objects of size n is equal to n times the number of objects of size n-1 plus the number of objects of size n-2.
Computing the recurrence relation is only possible if the specification is context free; FAIL is returned if this is not the case.
generateCode – automatic C code generation
(combinat::decomposableObjects(specification, <Options>))::generateCode(string filename)
Generate a C program in the file filename which can be used for efficient counting and random generation of objects.
To compile the program, the GMP library version 4.0 or higher is required; aside from this, any C compiler should work. Admitting that filename is blah.c, here is the command line for the gcc compiler: gcc blah.c -lgmp -o blah.
Once compiled, the program can be used completely independently from MuPAD with the command: blah n [k seed]. This writes to the standard output k random objects of size n (or FAIL if no object of size n exists), one per line. If k is 0, then the number of objects of size n is output instead. A third parameter seed can be provided to initialize the GMP random generator.
There are restrictions on the specifications that the C program can manage, in particular for complicated use of Alias. An error is raised if this is the case.
Currently the counting algorithm uses naive multiplication of generating series and whose time complexity is 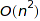 , and memory complexity
, and memory complexity 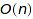 , not taking into account the coefficient growth. As for the "count" method, this could be reduced to
, not taking into account the coefficient growth. As for the "count" method, this could be reduced to 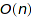 for context free grammars and to
for context free grammars and to 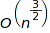 otherwise. The random generation algorithm is of complexity
otherwise. The random generation algorithm is of complexity 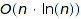 . For quasi-uniform random purpose, the counting could be done with floating point numbers (or better interval arithmetic), to ensure constant time arithmetic operations.
. For quasi-uniform random purpose, the counting could be done with floating point numbers (or better interval arithmetic), to ensure constant time arithmetic operations.
Example 1:
We create a domain for complete binary trees:
BinaryNaive:=combinat::decomposableObjects({B=Union(Z,Prod(B,B))}):
Standard form of specification
BinaryNaive::standardSpecification()

The number of binary tree of size 0 to 10
BinaryNaive::count(i) $i=0..10

A random tree of size 1 and size 2
BinaryNaive::random(i)$ i=1..2
List of all objects of size 4 satisfying the specification
BinaryNaive::list(4)
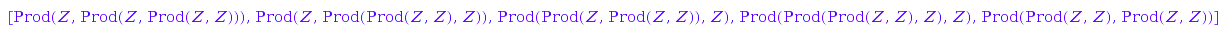
Example 2:
This specification is the Schroeder tree with Naive product:
SchroederNaive:=combinat::decomposableObjects(
{B=Union(Z,Prod(Z,B),Prod(Z,B,B))}):
Standard form of specification
SchroederNaive::standardSpecification()

The number of Schroeder tree of size 0 to 10
SchroederNaive::count(i) $i=0..10

A random tree of size 1 and size 2
SchroederNaive::random(i)$ i=1..2
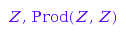
Example 3:
This specification defines the Schroeder trees with Naive and Holonomic product:
SchroederHolonomic:=combinat::decomposableObjects(
{B=Union(Z,Prod(Z,B),Prod(Z,B,B))},Products=Holonomic):
SchroederNaive:=combinat::decomposableObjects(
{B=Union(Z,Prod(Z,B),Prod(Z,B,B))}):
Time necessary to count the number of Schroeder tree of size 500 according to whether you use the holonomic products or not
time(SchroederNaive::count(500));time(SchroederHolonomic::count(500));
11340
30
Time necessary to generate a random Schroeder tree of size 500 according to whether you use holonomic products or not
time(SchroederNaive::random(500));
time(SchroederHolonomic::random(500));
820
490
Example 4:
We demonstrate how to use the functions generator and list.
Shroeder:=combinat::decomposableObjects(
{B=Union(Z,Prod(Z,B),Prod(Z,B,B))}):
Shroeder::count(5)

All objects of size 5 satisfying the specification
Shroeder::list(5)
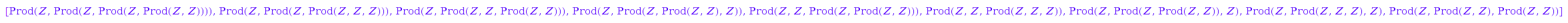
We build and use a generator for those objects:
f:=Shroeder::generator(5):
f() $ i =0..9
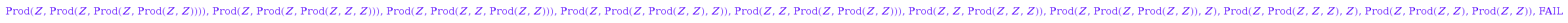
Example 5:
We create a domain for labeled and unlabeled complete binary trees:
BinaryUnlabeled:=combinat::decomposableObjects(
{B=Union(Z,Prod(B,B))},Labelled=FALSE):
BinaryLabeled:=combinat::decomposableObjects(
{B=Union(Z,Prod(B,B))},Labelled=TRUE):
Number of objects of size 0 to 10 satisfying the specification
BinaryUnlabeled::count(i)$i=0..10;
BinaryLabeled::count(i)$i=0..10;

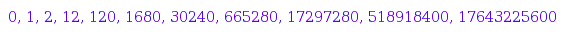
Example 6:
The grammar is not checked for validity. For example, the following grammar describes infinitely many objects of size zero (Prod(B,B), Prod(B, Prod(B,B)), Prod(B, Prod(B, Prod(...)))). The recursion formulas for counting are not well-founded, and MuPAD goes into an infinite loop when trying to compute the number of objects of size 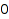 .
.
loop := combinat::decomposableObjects(
[A = Prod(B, Union(A, B)),
B = Epsilon(B)]):
loop::count(0):
Error: Recursive definition [See ?MAXDEPTH];
during evaluation of 'DOM_VAR(0,1)::count_functions[A]'
It would be better to emit a more meaningful error message; however, it is non trivial to check automatically whether a grammar is well-founded or not. For the moment, please consider any weird error message like the one above as a good indicator that the grammar might be invalid.
Example 7:
We use the mechanics of combinat::decomposableObjects to present the classical and striking “balls and bars” model for integer compositions. A composition like [2,1,3] can be represented as a string of balls and bars by using sequences of balls, separated by bars, here: "ooIoIooo". Such strings can be described by the grammar 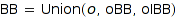 .
.
ballsAndBars :=
combinat::decomposableObjects(
[
Ball = Atom("o"),
Bar = Epsilon("I"),
BB = Union(Ball,
Alias(Prod(Ball, BB),op),
Alias(Prod(Ball, Bar, BB),op)
),
BallsAndBars = Alias(BB, _concat)
], MainNonTerminal = BallsAndBars):
There are 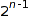 balls and bars strings with
balls and bars strings with 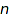 balls:
balls:
ballsAndBars::count(i) $ i = 1..10
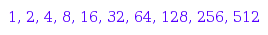
This can be seen directly from the recurrence relation:
ballsAndBars::recurrenceRelation()
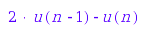
Here are all the compositions of 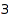 :
:
ballsAndBars::list(3)
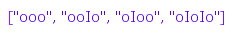
Example 8:
It is possible to do weighted enumeration by assigning weights to the atoms and epsilons. Then, the result of S::count(n) is the sum over each object of size n of the product of the weights of its atoms and epsilons.
In theory, it would be possible to use weights in any ring; however, this is an experimental feature, and there are some non documented restrictions on the rings. Also beware that the generating operations like "random", "unrank", "list" and "generator" rely on the standard definition of "count". So, a domain representing a decomposable combinatorial class can't be used simultaneously for advanced counting and for generation.
As a first application, we count unlabelled ordered trees by total number of nodes and number of internal nodes. To achieve this, we assign a weight of 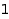 to leaves and of
to leaves and of  to internal nodes:
to internal nodes:
S :=
combinat::decomposableObjects(
[T = Union(Leaf, Prod(InternalNode, Sequence(T, MinLength = 1))),
Leaf = Atom(Leaf, 1),
InternalNode = Atom(InternalNode, q)],
CoeffRing = Dom::ExpressionField()):
The CoeffRing option specifies that the recurrence relation precomputations should take place in Dom::ExpressionField(). Now, S::count(n) computes the generating series by number of internal nodes of the trees with 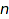 nodes altogether:
nodes altogether:
expand(S::count(4))
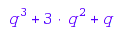
This means that, among the trees on 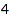 nodes, one has a single internal node, three have two internal nodes, and one has three internal nodes.
nodes, one has a single internal node, three have two internal nodes, and one has three internal nodes.
Another application of this feature is for doing approximate counting. To this end, we redefine the previous domain, but this time with a weight of 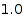 :
:
S :=
combinat::decomposableObjects(
[T = Union(Leaf, Prod(InternalNode, Sequence(T, MinLength = 1))),
Leaf = Atom(Leaf, 1.0),
InternalNode = Atom(InternalNode, 1.0)],
Products=Naive):
Now, count returns a floating point approximation of the number of objects having a given size:
[S::count(i) $ i = 0..10]

S::count(501)

The bonus is that approximate counting is much faster, as there is no coefficient growth. However, in order to use the fast holonomic counting method, it is safer to use exact arithmetic for precomputing the recurrence relation between, and only then to switch to approximate counting. This is what we do now:
S :=
combinat::decomposableObjects(
[T = Union(Leaf, Prod(InternalNode, Sequence(T, MinLength = 1))),
Leaf = Atom(Leaf, 1.0, 1),
InternalNode = Atom(InternalNode, 1.0, 1)]):
Note that the nodes now have two weights: one for approximate computations, and the other for exact computations. Of course those two weights should be coherent. Here is the recurrence relation obtained by the precomputation:
S::recurrenceRelation()
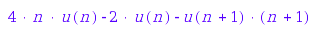
Now, one can compute quite large values:
S::count(20000)
7.900503708e12033
Alternatively, one can simply use the Float which does exactly this:
S :=
combinat::decomposableObjects(
[T = Union(Leaf, Prod(InternalNode, Sequence(T, MinLength = 1))),
Leaf = Atom(Leaf),
InternalNode = Atom(InternalNode)],
Float):
[S::count(i) $ i = 0..10]

A possible extension would be to allow the constructors like Prodto apply any transformation on the weights of their operands. A typical application of this is for computing the generating series of binary trees of a given size with respect to their maximal depth.
Background:
-
Not all functionalities (count, random, unrank, generator, list) are available for all constructors; some restrictions are documented above; otherwise, the system should emit an error if such a non available functionality is called.
-
In some cases, there is no known reasonable algorithm: this includes mainly unranking and uniform random generation of unlabelled Cycles, as well as random generation of labelled Powerset(A) without knowing how to unrank elements of A. Beware that the currently implemented random generation of unlabelled Cycles is not uniform; furthermore, randomly generated unlabelled Cycles and Sets are not normalized!
-
In most cases however, the functionalities are just not yet implemented. This library could also be extended and generalized in many other ways. Please contact the authors if you need some missing functionalities for your applications. Help would also be very welcome.
-
The Boustrophedonic option specifies the order in which elements of products are generated. To be specific, the objects of size 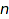 of a product Prod(A,B) are built from objects of A of size
of a product Prod(A,B) are built from objects of A of size 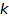 and objects of B of size
and objects of B of size 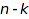 , for
, for 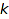 in
in  . The Boustrophedonic option controls in which order
. The Boustrophedonic option controls in which order 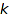 runs through
runs through  . If it is set to false, the straightforward order
. If it is set to false, the straightforward order 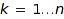 is used. Otherwise, the somewhat less natural order
is used. Otherwise, the somewhat less natural order 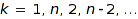 is used; it happens that this reduces the worst case complexity of the unranking and random generation operations from
is used; it happens that this reduces the worst case complexity of the unranking and random generation operations from 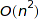 to
to 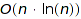 !
!
-
This library originates from the CS library for MuPAD 1.4 from Sylvie Corteel, Alain Denise, Isabelle Dutour, Frédéric Sarron and Paul Zimmermann. Parts of the documentation come from the GAIA package (ancestor of combstruct) by Paul Zimmermann.
-
References:
-
Flajolet, Philippe and Zimmermann, Paul and Van Cutsem, Bernard, A calculus for the random generation of labelled combinatorial structures, Theoretical Computer Science, 1994, 132, 1-2, pp. 1–35.
-
Denise, Alain and Dutour, Isabelle and Zimmermann, Paul, CS: a MuPAD package for Counting and Randomly Generating Combinatorial Structures, Proceedings of FPSAC'98, 1998, pp. 195–204.
-
Conrado Martinez and Xavier Molinero, Generic Algorithm for the Generation of Combinatorial Objects, 2003.
-
...
-
The specifications used by this library are in good parts compatible with those from the combstruct package for Maple. There are some differences though, in order to ensure the coherence with the rest of the MuPAD library: the constructor names Powerset and Multiset are used instead of respectively PowerSet and Set; furthermore, cardinality restrictions are stated as MinLength=3 instead of card>=3; finally, the Cycle construction includes the empty cycle. If needed, it would be straightforward to write a converter.
![]() :
: ![]() :
: ![]() :
: ![]() :
: ![]() :
: 
