Dom::TensorProductOfFreeModules – The domain of Tensor Product of Free Modules
Dom::TensorProductOfFreeModules([F1,F2,...]) create the tensor products of the free modules F1, F2.
→ Examples
Creating the Type
Dom::TensorProductOfFreeModules(ListF)
Parameters:
|
ListF:
|
a non empty list of free modules over the same coefficient ring R.
|
Details:
-
Dom::TensorProductOfFreeModules([F1,F2,...]) creates the tensor product of the free modules in [F1,F2,...]. The module must be modules over the same coefficient ring R over which the tensor product is taken.
-
The user don't need to create a Dom::TensorProductOfFreeModules. It is automatically created by a call to operators::tensor. However the overloading mechanism may slow down computations. Thus it may be faster to call directly the methods tensorConstructor and tensorConstructorFromSignature.
-
The system takes care of associativity, that is if some free modules in the list ListF are themselves tensor products, the list is flattened. More precisely, each element Fi of the list ListF is replaced recursively by it's entry Fi::modules. This is done before the creation of the domain. Consequently, the result of a constructor call Dom::TensorProductOfFreeModules(ListF) only depends on the flattening of ListF.
-
If dom1 is a tensor products, a valid signature is a list of free modules whose flattening is equal to M::modules. Several accessors can be constructed from a valid signature, a default is provided with the signature dom::modules.
-
A special combinatorial class dom::basisIndices is created to hold the indices. The elements of this class are Type::ListProduct(F1::basisIndices, F2::basisIndices, .... Currently, the system tries to build a grading for the combinatorial class dom::basisIndices from the grading of the Fi::basisIndices. This feature is experimental and may change in the future.
-
If all the Fi's are Cat::AlgebraWithBasis, the domain created is also a algebra from the category Cat::AlgebraWithBasis and the methods one, mult2Basis, mult2 and mult are defined accordingly. This feature is experimental and may change in the future.
-
The interface is not yet fully stable, they are several missing accessors.
Categories
Cat::ModuleWithBasis(R)
Entries
|
"modules"
|
the lists of modules whose dom is the tensor product. This list is flattened so that it contains no tensor products.
|
|
"basisIndices"
|
the combinatorial class baseClass of the indices of the basis.
|
tensorConstructorFromSignature – tensor constructor
(Dom::TensorProductOfFreeModules(ListF))::tensorConstructorFromSignature(signature lambda)
Returns a function which build a tensor product from list of elements of type Type::ListProductop(signature).
tensorConstructor – tensor constructor
(Dom::TensorProductOfFreeModules(ListF))::tensorConstructor(Type::ListProduct(op(dom::modules)) ListF)
Build the tensor products from the elements of the modules from the list ListF. This is the method tensorConstructorFromSignature called with the signature dom::modules.
toCartesianProductFromSignature – tensor analyzer
(Dom::TensorProductOfFreeModules(ListF))::toCartesianProductFromSignature(signature lambda)
Returns a function which returns a lists of Type::ListProduct(op(dom::modules)) from an element of dom.
toCartesianProduct – tensor analyzer
(Dom::TensorProductOfFreeModules(ListF))::toCartesianProduct(dom x)
Build a Cartesian products from an element of dom. This is the method toCartesianProductFromSignature called with the signature dom::modules.
Example 1:
Let us create some free modules and elements
f1 := Dom::FreeModule(Dom::Rational, combinat::words):
f2 := Dom::FreeModule(Dom::Rational, combinat::partitions):
e1 := f1([a, c, b]);
e2 := f2([3, 2, 1, 1]);
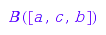
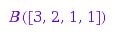
Let us compute a tensor product of two elements.
et := operators::tensor(e1, e2)
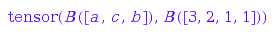
Its domain is:
tdom := domtype(et)
Error: Wrong type of 1. argument (type 'Type::Union(Cat::CombinatorialClass, Cat::Ring)' expected,
got argument 'combinat::words');
during evaluation of 'Dom::FreeModulePoly'
The element et can also be constructed by
et2 := tdom::tensorConstructor([e1, e2]);
bool(et = et2);
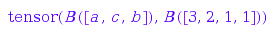

Changes in MuPAD 3.1
New Function.
![]()
![]()
![]()
![]()
![]()