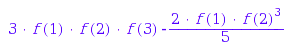of algebra generators. As for module generators (specified by "basis"), they are modelled by an associative combinatorial class; when 
, this can be as simple as a list of elements of the domain. Cat::AlgebraWithBasis – the category of associative algebras with a distinguished basis
Cat::AlgebraWithBasis(coeffRing) represents the category of associative algebras over the ring coeffRing with a distinguished basis.
Creating the Category
Cat::AlgebraWithBasis(coeffRing)
Parameters:
|
coeffRing: |
A domain which must be from the category Cat::Ring. |
Categories
Cat::Algebra(coeffRing), Cat::ModuleWithBasis(coeffRing)
Details:
A Cat::AlgebraWithBasis(coeffRing) is a coeffRing-algebra with a distinguished basis which is a combinatorial class in the category Cat::CombinatorialClass. The multiplication is typically implemented by extending by linearity its definition on the basis elements.
By default, the method "*" or "_mult" is set to operators::_mult, which in turn uses operators::mult2. Furthermore, the later is overloaded with the following signatures (in addition to the exiting ones, see Cat::ModuleWithBasis) and associated implementations:
[dom, dom] : "mult2"
[dom, coeffRing] : "multcoeffs"
[coeffRing, dom] : "multcoeffsLeft"
In other words, a Cat::AlgebraWithBasis(coeffRing) just has to implement the methods "mult2", "multcoeffs", and "multcoeffsLeft". Then, "_mult" is appropriately settled to handle all the possible ways it can be called in (binary and n-ary internal multiplications of elements, left and right multiplications by scalar, …). This differs from the plain Cat::Algebra category for which the domain has only to provide the "_mult" method. In a future version, this feature will be extended to Cat::Algebra.
The overloading mechanism may slow down computations. For example, if it is known that a, b are in a domain H in Cat::AlgebraWithBasis, then calling directly H::mult2(a,b) instead of a*b bypasses the overloading resolution and type coertions. This is highly recommended when optimising programs. Similarly it may be helpful to call directly H::multcoeffs and H::mult when appropriate. See also Cat::ModuleWithBasis for more optimizations.
Entries
|
"oneBasis" |
If the unit of the algebra is a basis element, the index of this basis element can be provided here, instead of defining "one". |
fromCoeffRing – natural embedding of the coefficient ring
Cat::AlgebraWithBasis::fromCoeffRing(coeffRing c)
Returns the natural embedding c*dom::one of the coefficient c as an element of this algebra.
ground – ground coefficient
Cat::AlgebraWithBasis::ground(dom x)
Returns the ground coefficient of x, that is the coefficient of x on the unit of the algebra.
This only makes sense if the unit of the algebra is a basis element, so this method is optional. A default implementation is provided when "oneBasis" is defined.
Mathematical Methods
mult2Basis – binary multiplication of basis elements
Cat::AlgebraWithBasis::mult2Basis(dom::basisIndices x, dom::basisIndices y)
Returns the product of two basis elements indexed by x and y.
The default implementation is "multBasis"; so, the domain may define either one of them, or both, at the programmer's convenience.
mult2 – binary multiplication
Cat::AlgebraWithBasis::mult2(dom x, dom y)
Returns the product of x by y.
x and y are required to be of this domain; no coercion is attempted.
The default implementation extends "mult2Basis" by bilinearity.
multBasis – n-ary multiplication of basis elements
Cat::AlgebraWithBasis::multBasis(<dom::basisIndices x, ...>)
Returns the product of the basis elements indexed by the arguments.
If no argument is provided, it returns the unit of the algebra (dom::one).
mult – n-ary multiplication
Cat::AlgebraWithBasis::mult(<dom x, ...>)
Returns the product of the arguments. If no argument is provided, it returns the unit of the algebra (dom::one).
The arguments are required to be of this domain; no coercion is attempted.
The default implementation extends "mult2" by associativity. Sometime in the future, it may instead extend "multBasis" by multilinearity.
Algebra generators
An algebra with basis may provide a family of algebra generators. As for module generators (specified by "basis"), they are modelled by an associative combinatorial class; when , this can be as simple as a list of elements of the domain.
If a procedure "algebraToList" or "algebraToListSparse" is implemented to rewrite any element of the algebra in terms of the generators, then the user will be able to use "algebraMorphism" to easily construct algebra morphisms from their values on the algebra generators.
algebraToList – expression of an element in terms of the algebra generators
Cat::AlgebraWithBasis::algebraToList(dom x)
Expresses the element x as a linear combination of products of the algebra generators (very much like toList(x) describes an expression of x as a linear combination of the module generators). The result needs not be unique.
Technically, this method returns a list of terms of the form [coefficient, list of indices of generators]. Cf. example 3.
In the long term, it will be possible to use specialized more compact data structures for the result, typically in the case of commutative algebras.
This method is optional.
algebraMorphism – algebra morphism from value on generators
Cat::AlgebraWithBasis::algebraMorphism(function f, <Options>)
Options:
|
ImageSet = A: |
The algebra which f maps to. |
|
Plus = plusM: |
The function used for additions. Defaults to M::plus or _plus. |
|
Zero = |
The zero of M. Defaults to M::zero or |
|
Mult = multM: |
The function used for multiplications. Defaults to M::mult or _mult. |
|
One = oneM: |
The one of A. Defaults to A::one or |
|
Multcoeffs = mc: |
The function used for multiplication by scalar. Defaults to A::multcoeffs or multcoeffs. |
Returns the algebra morphism defined from the values of f on the algebra generators of dom.
f must be a function from the indices of the generators of this domain (dom::algebraGenerators::keys) to some coeffRing-algebra A. Cf. example 3.
This method is implemented by this category as soon as "algebraToList" or "algebraToListSparse" is defined.
In case dom is not a free algebra over "basisIndices", it is the user's responsibility to make sure that f is compatible with the algebra-relations, and does indeed define a proper module morphism.
This function relies on the proper implementation of "algebraToList".
In case coeffRing is non commutative, beware that multcoeffs multiplies by scalars on the right, whereas the standard pretty printing of module elements suggests that the scalar coefficients are considered as being on the left of the basis elements. This inconsistency will be fixed one way or the other in a later release. In the meantime, you may use Multcoeffs= M::multcoeffsLeft to force the multiplication to be done on the left.
algebraClosure – sub-algebra generated by a set of generators
Cat::AlgebraWithBasis::algebraClosure(list generators, <Options>)
Returns a basis, in reduced echelon form, of the (non-unital) subalgebra generated by the elements in generators
To obtain the unital subalgebra instead, simply include dom::one to the list of generators; later on, there will some Unital option to take care of this situation more efficiently.
We define the algebra of the symmetric group on 4 elements:
domain SymmetricGroupAlgebra(N: Type::NonNegInt)
inherits Dom::FreeModule(Dom::ExpressionField(),
combinat::subClass(combinat::permutations,
Parameters=N));
category Cat::AlgebraWithBasis(Dom::ExpressionField());
oneBasis := [$1..N];
mult2Basis := dom::term @ combinat::permutations::_mult;
end_domain;
A4 := SymmetricGroupAlgebra(4):
Now, we create some elements of A4, and do some simple computations with them:
a := A4::one;
a + a;
A4([1,2,3,4]) - A4::one;
a := A4([2,3,4,1]);
a^2;
a^4;
Here are some more advanced computations:
3*a + 4/5*A4([1, 3, 2, 4])
a^2*x + (a*y)^3 + A4::one + A4([3, 2, 1, 4])*z
Now we demonstrate how to do some basic linear algebra, say to find the minimal polynomial of an element of A4. For the sake of simplicity, we assume that we know in advance that the minimal polynomial is of degree 
:
a := A4([2,3,1,4]);
P := x0*X^0 + x1*X^1 + x2*X^2 + X^3;
b := subs(P, X=a);
solution := linsolve([coeff(b)], [x0,x1,x2]);
subs(P, solution);
We now demonstrate how to construct algebra morphisms. Consider the free algebra with generators indexed by 1,2,...:
domain FreeAlgebra
inherits Dom::FreeModulePoly(Dom::Rational, combinat::compositions);
category Cat::AlgebraWithBasis(Dom::Rational);
oneBasis := [];
mult2Basis := dom::term @ _concat;
algebraGenerators := combinat::classes::indexed(Dom::Natural, // almost
i->dom::term([i]));
algebraToList := dom::toList;
end_domain:
Here is a typical element of this free algebra:
x := 3*FreeAlgebra([1, 2, 3]) - 2/5*FreeAlgebra([2, 1, 2, 2]);
and its (straightforward) representation in terms of the generators:
FreeAlgebra::algebraToList(x)
The algebra morphism from the FreeAlgebra to the field of expressions, mapping the 
-th generator to the symbolic function call f(i) can now be constructed with:
g := FreeAlgebra::algebraMorphism(hold(f), ImageSet = Dom::ExpressionField()):
g(x)
