Cat::ModuleWithBasis – the category of modules with a distinguished basis
Cat::ModuleWithBasis(coeffRing) represents the category of modules with a distinguished basis.
→ Examples
Creating the Category
Cat::ModuleWithBasis(coeffRing)
Parameters:
|
coeffRing:
|
A domain which must be from the category Cat::Ring.
|
Categories
Cat::Module(coeffRing)
Details:
-
A domain of the category Cat::ModuleWithBasis(coeffRing) is a domain of the category Cat::Module(coeffRing) where coeffRing is a Cat::Ring, with a distinguished basis indexed by some combinatorial class baseClass in the category Cat::CombinatorialClass. This means that there exists a family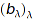 
of elements of the module such that any element 
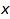of the module can be represented as a (formal) linear combination 
with coefficients 
in coeffRing. The linear combination may be finite or infinite, and two syntactically different linear combinations may be mathematically equal.
-
If coeffRing is in Cat::Field then Cat::ModuleWithBasis inherits from the category Cat::VectorSpace(coeffRing) instead of Cat::Module.
-
Cat::ModuleWithBasis(coeffRing) is the basic super category for anything “that looks like a polynomial or a series.” This includes for example differential operators or forms, Ore polynomials, elements of combinatorial algebras, and so on.
-
The support of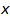 
is the set of all 
s such that 
. The terms and monomials of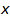 
are respectively the 
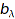s and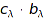 
s such that 
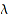is in the support of 
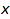. The operands of 
are its monomials, each monomial being represented by an object whose first operand is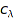 
and second operand is 
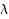. The standard accessors op and nops are defined accordingly.
-
Depending on the domain, the term order may come from the combinatorial class or be a totally irrelevant internal order. The leading support, term, and monomial (and their trailing equivalents) are defined in the natural way by extending the usual notions for polynomials. They need not exist when 
has an infinite support.
-
By default, the method "*" or "_mult" is set to operators::_mult, which in turn uses operators::mult2 (to multiply two elements). Furthermore, the later is overloaded with the following signatures and associated implementations:
-
[dom, coeffRing] : "multcoeffs"
-
[coeffRing, dom] : "multcoeffsLeft"
In other words, a domain in Cat::ModuleWithBasis should provide the implementation of "multcoeffs" and "multcoeffsLeft". Then, "_mult" is appropriately settled to handle both left and right multiplication by scalars. This differs from the plain Cat::Module category for which the domain has to provide this "_mult" method. In a future version, this feature will be extended to Cat::Module.
-
Default implementations are provided for most of the methods; they can be quite inefficient though, so it is highly recommended to redefine them. At the very least, the domain just needs to implement the constructor "monomial", and the methods "toList" and "coeff".
-
The overloading mechanism may slow down computations. For example, if it is known that a, b are in a domain H in Cat::ModuleWithBasis, then calling directly H::plus2(a,b) instead of a+b bypasses the overloading resolution and type coertions. This is highly recommended when optimising programs. Similarly it may be helpful to call directly H::multcoeffs and H::multcoeffsLeft when appropriate. In a same way, if x is a H::basisIndices and a is a H::coeffRing then, for creating elements, H::term(x) is faster than H(x) and H::monomial(c, x) is faster than c*H(x) and H::multcoeffsLeft(c, H::term(x)).
Entries
|
"basisIndices"
|
the combinatorial class baseClass of the indices of the basis; it must be a Cat::CombinatorialClass.
|
|
"zero"
|
the zero element
|
term – term constructor
Cat::ModuleWithBasis::term(baseClass lambda)
Returns the basis element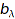 
indexed by the element lambda of the combinatorial class baseClass.
monomial – monomial constructor
Cat::ModuleWithBasis::monomial(coeffRing c, baseClass lambda)
Returns the monomial 
indexed by the element lambda of baseClass with coefficient c.
fromList – constructor from list
Cat::ModuleWithBasis::fromList(l)
l should be a list of the form 
, where 
belong to coeffRing and 
are elements in baseClass. This list does not need to be sorted in any way, and the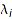 
s are not required to be distinct.
Returns the linear combination 
described by the list.
This method is very similar to the creation of MuPAD polynomials from a list.
toList – list
Cat::ModuleWithBasis::toList(dom x)
Returns a list describing the structure of x.
This is the inverse function of "fromList".
This method is very similar to the poly2list method for MuPAD polynomials.
nterms – number of terms
Cat::ModuleWithBasis::nterms(dom x)
Returns the number of terms of x.
support – support
Cat::ModuleWithBasis::support(dom x)
Returns the support of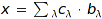 
; that is, the list of all 
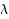s such that 
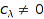. It returns a list of elements of baseClass whereas terms (see below) gives a list of elements of dom.
terms – terms
Cat::ModuleWithBasis::terms(dom x)
Returns the list of the terms of 
; that is, the list of all 
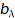s such that 
. It returns a list of elements in dom, whereas support gives a list of elements of baseClass.
monomials – monomials
Cat::ModuleWithBasis::monomials(dom x)
Returns the list of the monomials of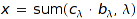 
; that is, the list of all 
.
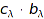coeffs – coefficients
Cat::ModuleWithBasis::coeffs(dom x)
Returns the list of all the non-zero coefficients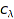 
of x.
coeff – coefficient(s)
Cat::ModuleWithBasis::coeff(dom x)
Cat::ModuleWithBasis::coeff(dom x, baseClass lambda)
Returns the sequence of all the non-zero coefficients 
of x.
Returns the coefficient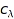 
of x at the index lambda.
_lessBasis – Term order on basis elements
Cat::ModuleWithBasis::_lessBasis(baseClass lambda1, baseClass lambda2)
Compare the two basis elements lambda1 and lambda2, returning TRUE if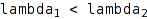 
and FALSE otherwise.
This must be compatible with the term order used in "lterm", "poly2list", and so on. The (slow) default implementation guarantees this.
lsupport – support of the leading term
Cat::ModuleWithBasis::lsupport(dom x)
Returns the support of the leading term of x.
If x is zero, then FAIL is returned.
lterm – leading term
Cat::ModuleWithBasis::lterm(dom x)
Returns the leading term of x.
If x is zero, then the zero of the domain is returned. This convention ensures the compatibility with standard MuPAD polynomials.
lmonomial – leading monomial
Cat::ModuleWithBasis::lmonomial(dom x)
Returns the leading monomial of x.
If x is zero, then the zero of the domain is returned. This convention ensures the compatibility with standard MuPAD polynomials.
lcoeff – leading coefficient
Cat::ModuleWithBasis::lcoeff(dom x)
Returns the leading coefficient of x.
If x is zero, then the zero of the coefficient ring is returned.
tsupport – support of the trailing term
Cat::ModuleWithBasis::tsupport(dom x)
Returns the support of the trailing term of x.
If x is zero, then FAIL is returned.
tterm – trailing term
Cat::ModuleWithBasis::tterm(dom x)
Returns the trailing term of x.
If x is zero, then the zero of the domain is returned. This convention ensures the compatibility with standard MuPAD polynomials.
tmonomial – trailing monomial
Cat::ModuleWithBasis::tmonomial(dom x)
Returns the trailing monomial of x.
If x is zero, then the zero of the domain is returned. This convention ensures the compatibility with standard MuPAD polynomials.
tcoeff – trailing coefficient
Cat::ModuleWithBasis::tcoeff(dom x)
Returns the trailing coefficient of x.
If x is zero, then the zero of the coefficient ring is returned.
nthsupport – support of the n-th term
Cat::ModuleWithBasis::nthsupport(dom x, Type::PosInt n)
Returns the support of the n-th term of x.
If n exceeds strictly the number of terms of x, then FAIL is returned.
nthterm – n-th term
Cat::ModuleWithBasis::nthterm(dom x, Type::PosInt n)
Returns the n-th term of x.
If n exceeds strictly the number of terms of x, then FAIL is returned.
nthmonomial – n-th monomial
Cat::ModuleWithBasis::nthmonomial(dom x, Type::PosInt n)
Returns the n-th monomial of x.
If n exceeds strictly the number of terms of x, then FAIL is returned.
nthcoeff – n-th coefficient
Cat::ModuleWithBasis::nthcoeff(dom x, Type::PosInt n)
Returns the n-th coefficient of x.
If n exceeds strictly the number of terms of x, then FAIL is returned.
mapcoeffs – apply a function to all the coefficients
Cat::ModuleWithBasis::mapcoeffs(dom x, function f, <opt1, ...>)
Returns a copy of x in which each coefficient c has been replaced by f(c, opt1, …).
f should always return elements of the coefficient ring. For efficiency reasons, this is not necessarily checked.
multcoeffs – (right) multiplication of all coefficients by a scalar
Cat::ModuleWithBasis::multcoeffs(dom x, coeffRing c)
Returns a copy of x where all the coefficients have been multiplied (from the right) by c.
multcoeffsLeft – left multiplication of all coefficients by a scalar
Cat::ModuleWithBasis::multcoeffsLeft(dom c, coeffRing x)
Returns a copy of x where all the coefficients have been multiplied from the left by c.
If coeffRing is commutative, multcoeffsLeft and multcoeffs coincide.
mapsupport – apply a function on all elements of the support
Cat::ModuleWithBasis::mapsupport(dom x, function f, <opt1, ...>)
Returns a copy of x in which each element c of the support has been replaced by f(c, opt1, …).
f should always return elements in coeffRing. For efficiency reasons, this is not necessarily checked.
content – content
Cat::ModuleWithBasis::content(dom x)
computes the content of x, i.e., the gcd of all its coefficients.
This method only exists if coeffRing is a domain of category Cat::GcdDomain.
moduleMorphism – extension by linearity
Cat::ModuleWithBasis::moduleMorphism(function f, <Options>)
Parameters:
|
f:
|
A function from the basis of this domain (basisIndices) to some coeffRing-module M.
|
Options:
|
ImageSet = M:
|
The module M
|
|
Plus = plusM:
|
The function used for additions in M. Defaults to M::plus or _plus.
|
|
Zero = zeroM:
|
The zero of M. Defaults to M::zero or 0.
|
|
Multcoeffs = multM:
|
The function used for multiplication by scalar. Defaults to M::multcoeffs or multcoeffs.
|
dom::moduleMorphism returns the module morphism from dom to M obtained by extending f by linearity.
In case dom is not a free module over "basisIndices", it is the user's responsibility to make sure that f is compatible with the module-relations, and does indeed define a proper module morphism.
In case coeffRing is non commutative, beware that multcoeffs multiplies by scalars on the right, whereas the standard pretty printing of module elements suggests that the scalar coefficients are considered as being on the left of the basis elements. This inconsistency will be fixed one way or the other in a later release. In the meantime, you may use Multcoeffs = M::multcoeffsLeft to force the multiplication to be done on the left.
Example 1:
We demonstrate how to define module morphisms on the free module M over the rationals with basis indexed by words. We start by constructing a function which maps a word to the basis element of M indexed by its reverted word:
M := Dom::FreeModule(Dom::Rational, combinat::words):
f := M::term @ revert:
f([a, b, c])
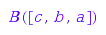
Now, we can extend f by linearity to a module morphism from M to M:
g := M::moduleMorphism(f, ImageSet=M):
x := 3*M([a, b, c]) - 2*M([a, e]);
g(x)
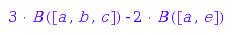
Note that, for a simple endomorphism like this one, we could have achieved the same effect with mapsupport:
M::mapsupport(x, revert)
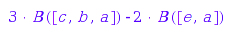
Funny and sometimes interesting results may be achieved by specifying manually the operations to be used for addition and scalar multiplication. Here is an example:
g := M::moduleMorphism(hold(f), ImageSet = Dom::ExpressionField(),
Plus = hold(plus), Multcoeffs = hold(s)):
g(x)
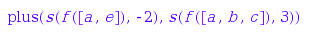
In particular, this can be used to define a module morphism to a module having a different (but compatible) coefficient ring:
M2 := Dom::FreeModule(Dom::IntegerMod(7), combinat::words):
f := M2::term@revert:
g := M::moduleMorphism(f, ImageSet = M2, Multcoeffs=_mult):
g(x)
