polylib::coeffRing – coefficient ring of a polynomial
polylib::coeffRing(p) returns the coefficient ring of p.
Calls:
polylib::coeffRing(P)
polylib::coeffRing(p)
Parameters:
|
P: |
a polynomial domain or free module |
|
p: |
a polynomial or free module element |
Return Value:
A domain
Details:
polylib::coeffRing(p) allows to query in a uniform way the coefficient ring of the polynomial p or the polynomial domain P.
P can be a polynomial domain (Dom::UnivariatePolynomialx, Dom::DistributedPolynomial[x,y], ...), or more generally some module with basis (Cat::ModuleWithBasis).
P can also be of the form polylib::Poly([x,y],K). If K is Expr or IntMod(n), then the corresponding domains Dom::ExpressionField() or Dom::IntegerMod(p) is returned. See poly for the details about Expr and IntMod(n).
p can be a kernel polynomial (DOM_POLY), or an element of one of the above domains
We define a polynomial ring over the ring of integers modulo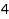 
, and query for its coefficient ring:
P := Dom::UnivariatePolynomial(x, Dom::IntegerMod(4)):
polylib::coeffRing(P)
The coefficient ring of the elements of this domain can be queried the same way:
polylib::coeffRing(P(x))
polylib::coeffRing(Dom::Matrix(Dom::IntegerMod(3)))
When no coefficient ring is specified, poly currently constructs kernel polynomials over the fake domain Expr instead of the mathematically equivalent field Dom::ExpressionField() of arbitrary expression (this happens to be more efficient with the current kernels):
extop(poly(x))
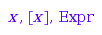
polylib::coeffRing(poly(x))
This makes it possible to plug the result right away as coefficient ring of some other domain:
Dom::UnivariatePolynomial(x, polylib::coeffRing(poly(x)))
