-
Given a combinatorial class class such that the standard function takes some parameters, one often wants to consider a new combinatorial class where this parameter is fixed. For example, if one wants to consider the class of words on a fixed alphabet. This is the purpose of combinat::subClass.
-
The simplest case of usage is for example when one need to build the finite class of all element of a given size n for an infinite class say combinat::compositions. In this case, the subclass is created by a call subclass := combinat::subClass(combinat::compositions, Parameters=n) Then the call subclass::list() is computed automatically by a call to combinat::compositions::list(n) and a call to subclass::unrank(r) is computed by a call to combinat::compositions::unrank(r, n). Note that optional extra parameters still need to be passed after n as in subclass::list(MaxLength=3) which is computed by combinat::compositions::list(n, MaxLength=3).
-
In more advanced examples, the parameter mangling is more complicated than simply add an extra parameter after the standard one. in this case, one use the option Parse which allows to pass a function that takes care of the parameter mangling.
-
One distinguish between two kinds of methods of the subclass. The first kind are the standard methods such as isA, count or list for which the extra parameters need to be passed. The second kind are the other method that are simply copied from class.
The first kind of methods is defined by the InheritsWithParameters and is by default ["count", "list", "generator", "first", "last", ["isA", 1], ["unrank", 1]]. The one after isA and unrank is here because there is one parameter in front of the extra parameter for these two functions.
The second kind is defined InheritsWithoutParameters and is by default ["convert", "expr", "print"].
-
In one wants that the created class has a notion of size, one can provide the function through the option Size. In this case, the created class belongs to Cat::GradedCombinatorialClass
-
The created class is a facade domain so there is no need to create directly element of this class, in particular, no constructor is defined.
-
This class is still in design and the interface may change in the future versions.
Let us consider the class of subsets of 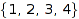 :
:
st4 := combinat::subClass(combinat::subsets, Parameters=4)

Then the interface of st4 is compatible with Cat::CombinatorialClass. It is therefore now possible to ask for the lists the elements of st4:
st4::list()
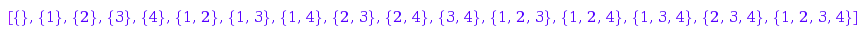
Or else to list those of a give size:
st4::list(2)
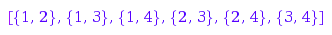
One can also ask if a given set is a subset:
st4::isA({1,2,4});
st4::isA({1,2,6});


One problem is that the system cannot generate automatically a notion of size:
st4::size({1,2,4});

This is easily fixed by
st4Ok := combinat::subClass(combinat::subsets, Parameters=4, Size=nops);
st4Ok::size({1,2,4});


Note that on the contrary to the class st4, the class st4Ok is graded:
st4::hasProp(Cat::GradedCombinatorialClass);
st4Ok::hasProp(Cat::GradedCombinatorialClass);
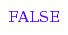

In some cases a more complicated argument mangling is needed. Suppose that we want to build a class for integer vectors of a given length say 3. This is needed of one wants to build a free module over this basis, for example the polynomials in three variables. The problem arise because combinat::integerVectors take the sum as first argument and the length as second argument. By default, the argument passed to combinat::subClass are put in front of the argument list. Thus we have to use the option Parse:
iv3 := combinat::subClass(combinat::integerVectors,
Parse = (z -> (z, 3, args(2..args(0)))),
Size = (z -> _plus(op(z)))):

The iv3 is a correct combinatorial class:
iv3::list(3)

Extra parameters are still correctly managed:
iv3::list(7, MinPart=2)
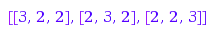
There is still a slight problem with the function isA:
iv3::isA([1,2,2]);
iv3::isA([1,2,2],6);
Warning: Uninitialized variable 'z' used;
during evaluation of 'x'
Error: Wrong type of 2. argument (type 'Type::Union(DOM_FAIL, Type::NonNegInt)' expected,
got argument 'NIL');
during evaluation of 'combinat::integerVectors::isA'
This is due to the fact that for combinat::integerVectors it is not possible to pass the lenght to isA without passing the size. Therefore one needs to redefine isA. The best way is to inherits from combinat::subClass. Here is a complete example:
domain integerVectorsOfLength(N : Type::NonNegInt)
inherits combinat::subClass(combinat::integerVectors,
InheritsWithParameters = ["count", "list", "generator"],
Parse = (z -> (z, N, args(2..args(0)))),
Size = (z -> _plus(op(z))));
category Cat::GradedCombinatorialClass,
Cat::FacadeDomain(combinat::integerVectors);
info_str := "the combinatorial class of integer vectors of fixed length";
isA :=
proc(obj : Type::AnyType,
deg = null() : Type::Union(DOM_NULL, Type::NonNegInt))
begin
if args(0) = 1 then
_lazy_and(combinat::integerVectors::isA(obj), nops(obj) = N);
else combinat::integerVectors::isA(obj, deg, N);
end_if;
end_proc;
end_domain:
iv3 := integerVectorsOfLength(3):
iv3::isA([1,2,2]);
iv3::isA([1,2,2,3]);
iv3::isA([1,2,2],5);
iv3::isA([1,2,2],6);

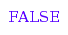

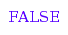
Let do a few more checks:
iv3::count(4);

iv3::list(4);
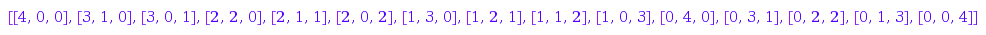
![]() :
: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()