combinat::setPartitionsOrdered – ordered set partitions of a set
The library combinat::setPartitionsOrdered provides functions for counting, generating, and manipulating ordered set partitions.
→ Examples
Related Domains:
combinat::compositions, combinat::setPartitions
Details:
An ordered set partition p of a set s is a partition of s, into subsets called parts and represented as a list of sets. By extension, an ordered set partition of a nonnegative integer n is the set partition of the integers from 1 to n. The number of ordered set partitions of n is called the n-th ordered Bell number.
There is a natural integer composition associated with an ordered set partition, that is the sequence of sizes of all its parts in order.
Entries
|
"domtype"
|
The MuPAD domain used to represent set partitions: DOM_LIST
|
isA – test if an object is an ordered set partition
combinat::setPartitionsOrdered::isA(any type set, <set s, composition c>)
Returns whether set is an ordered set partition.
If the first optional argument s is present, returns whether set is an ordered set partition of s.
If the second optional argument c is present, returns whether set is a set partition of swith parts of sizes given by c.
count – number of ordered set partitions
combinat::setPartitionsOrdered::count(any type set, <composition c>)
Returns the number of ordered set partitions of set whose underlying composition is c.
list – list of ordered set partitions
combinat::setPartitionsOrdered::list(any type set, <composition c>)
Returns the list of ordered set partitions of set whose underlying composition is c.
Example 1:
There are 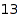 ordered set partitions of
ordered set partitions of 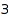 :
:
combinat::setPartitionsOrdered::count(3)

Here is the list:
combinat::setPartitionsOrdered::list(3)
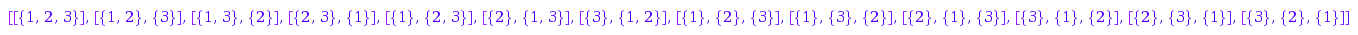
There are 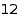 set partitions of
set partitions of 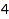 whose underlying partition is
whose underlying partition is 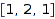 :
:
combinat::setPartitionsOrdered::list(4,[1,2,1])
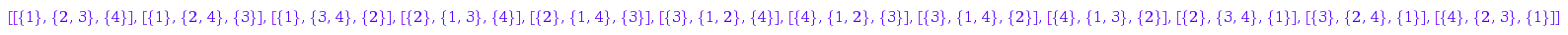
![]() ordered set partitions of
ordered set partitions of ![]() :
:![]()
![]()
![]() set partitions of
set partitions of ![]() whose underlying partition is
whose underlying partition is ![]() :
:![]()