combinat::countingFunctions

Here, we call counting function

a function from the non negative integers to themselves. Typically

counts the number of objects of size

in a given graded combinatorial class. Otherwise said,

is the

-th coefficient of the generating series associated to the combinatorial class.

Counting functions are often used to count the dimensions of the homogeneous components of a graded vector space. In this case the generating series becomes the Hilbert series of that vector space.

A functor takes one or several counting functions and returns a new counting function. For example, if f counts the objects of a combinatorial class

the functor set returns the counting function for the sets of objects of

. Most functors correspond to operations on combinatorial classes, or on the corresponding generating series

, or on graded vector spaces.

This library essentially provides classical functors for counting functions. Most of those functors actually work more generally with functions from the non-negative integers to some ring.

To define the semantic of all the algebraic functors below ("_mult", "int", ...), we always interpret a counting function

as its corresponding univariate generating series

This library is intended as a repository of fast and flexible low-level utilities, upon which higher level interfaces can be built (say in the form of generating series).

All complexity results are given in number of arithmetic operations on the coefficient ring, and do not include the cost of the computation of the counting functions passed as arguments.

This corresponds to the product

of generating series, the cartesian product of graded combinatorial classes, or the tensor product of graded vector spaces.

Complexity:

for computing the

first coefficients. In the short term, this complexity will be reduced to

using a lazy-Karatsuba algorithm; an experimental implementation of this algorithm is readily available under the name mult2Karatsuba although with a still large constant time factor. In theory, the complexity could be further reduced to essentially

using FFT.

Returns the counting function for the generating series

by the exponential function.

Returns the counting function f with all coefficients shifted by delta. In case delta is positive, the missing coefficients of f are completed with zeroes of the coefficient ring.

Algebraically, when delta is non-negative, this is the counting function for

. When delta is negative, the same formula holds after discarding the first terms of

. For example, shifting

yields

Returns the counting function for the unique primitive

having constant term

Returns the counting function for the Laplace transform of the generating series F(z).

Returns the counting function for the inverse Laplace transform of the generating series F(z).

Assuming that f counts the objects of a combinatorial class

, this returns the counting function for the sequences of objects of

Assuming that f counts the algebra generators of a graded free algebra

, this returns the Hilbert series

Assuming that f counts the objects of a combinatorial class

, this returns the counting function for the sets of objects of

without repetitions.

Assuming that f counts the algebra generators of a graded free exterior algebra

, this returns the Hilbert series

Assuming that f counts the objects of a combinatorial class

, this returns the counting function for the multisets of objects of

Assuming that f counts the algebra generators of a graded free commutative algebra

, this returns the Hilbert series

. The same property holds for the enveloping algebra of a Lie algebra.

Assuming that f counts the objects of a combinatorial class

, this returns the counting function for the cycles of objects of

Assuming that f counts the objects of a combinatorial class

, this returns the counting function

for the Lyndons words of objects of

(that is aperiodic cycles of objects of

Assuming that f counts the Lie generators of a graded free Lie algebra

, this returns the Hilbert series

combinat::countingFunctions::plethysmPowersum(counting function f, non negative integer k)

Returns the plethysm of f by the k-th symmetric powersum (this corresponds to the generating series

This corresponds to the generating series:

. Combinatorially, this corresponds to the subst operation.

combinat::countingFunctions::plethysmSym(symmetric function g, counting function f)

Returns the plethysm of f by the symmetric function g. This is obtained by expressing g in terms of symmetric powersums, and using plethsymPowersum.

We start from one of the simplest counting function:

f := n -> 1:

f(n) $ n = 0..10

This counting function corresponds to the combinatorial class of natural integers:

Dom::Natural::count(n) $ n = 0..10

and to the generating series :

series(1/(1 - z), z, 11)

We construct the product of f by itself:

g := combinat::countingFunctions::mult2(f, f):

g(n) $ n = 0..10

It corresponds to the Cartesian product of the set of natural integers by itself. Namely, f(n) counts the couples of non-negative integers, w.r.t. their sum :

combinat::integerVectors::list(4, 2);

combinat::integerVectors::count(n, 2) $ n = 0..10

Note that this Cartesian product can also be explicitly constructed by means of combinat::decomposableObjects:

C := combinat::decomposableObjects([ C = Prod(Domain(Dom::Natural), Domain(Dom::Natural)) ]):

C::list(4);

C::count(n) $ n = 0..10

The counting function g also corresponds to the generating series :

series( 1 / (1 - z)^2, z)

Now, a more interesting example: applying the "multiset" functor on (where represents the unit counting function) counts multisets of positive natural numbers, that is integer partitions:

g := combinat::countingFunctions::multiset(f-combinat::countingFunctions::one):

g(n) $ n = 0..10;

combinat::partitions::count(n) $ n = 0..10

Note that those are the dimensions of the homogeneous components of the free commutative algebra with one generator per degree, that is the ring of symmetric functions.

Similarly, applying the "powerset" functor counts strictly decreasing integer partitions:

g := combinat::countingFunctions::powerset(f-combinat::countingFunctions::one):

combinat::partitions::count(n, MaxSlope = -1) $ n = 0..10;

g(n) $ n = 0..10

Counting functions are not typed as such. In fact one can use as counting function any MuPAD object which behaves as a function from the integers to some ring. Typically, in the previous example, the function n->1 can be replaced by just 1:

f := 1:

f(n) $ n = 0..10

Another application is to use symbolic functions to produce symbolic formulas for the functors:

delete(f): delete(g):

h := combinat::countingFunctions::mult2(f, g):

h(4)

h := combinat::countingFunctions::multiset(f):

h(2)

math

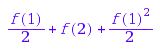
h := combinat::countingFunctions::powerset(f):

h(2)

math

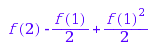
h := combinat::countingFunctions::laplace(f):

h(i) $ i = 0..6

There is a price to pay for the speed and flexibility of this low-level design. Namely, writing f*g does not call the product of counting functions. Instead, it returns the point-wise product of f by g (which corresponds to the Hadamard product of generating series):

h := f * g:

h(n) $ n = 0..4

"coeffRing"	The coefficient ring, that is Dom::ExpressionField().
"zero"	The zero counting function, which maps all natural numbers to 0.
"one"	The unit w.r.t. the product of counting functions. This is the function which maps 1 to 1 and all other natural numbers to 0.