operators::overloaded – conversions and overloaded functions
The library operators::overloaded provides a framework for conversions between domains. It also allows for defining multiparameter overloaded functions.
→ Examples
Creating Elements
operators::overloaded(default, <signatures>)
Parameters:
|
default:
|
A function.
|
|
signatures:
|
A table associating implementations to signatures.
|
Details:
-
operators::overloaded(default, signatures) returns a new overloaded function, with default as default implementation, and with signatures and corresponding implementations taken from signatures.
-
In the first place, operators::overloaded is a library which allows for declaring and using conversions between MuPAD domains. Those conversions can be implicit or explicit.
-
Implicit conversions can be used automatically by the system, for example in overloaded function calls (see below). They are applied transitively: if there is a conversion from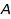 
to 
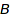, and one from 
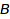to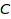 
, then this provides by composition a conversion from 
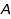to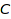 
; we call this a composite conversion.
-
At any given time, there is at most one conversion between two domains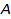 
and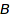 
. On the other hand there may be several possible composite conversions. To resolve this, implicit conversions have an associated weight which is additive versus composition. This weight is supposed to represent a rough evaluation of the cost of the conversion. When two composite conversions are possible, one with minimal weight is chosen.
-
Explicit conversions are only applied when requested explicitly (see operators::overloaded::convertExplicit). They are not applied transitively.
-
operators::overloaded is also a domain whose objects are multi-parameter overloaded functions f, which may have several simultaneous implementations with associated signatures (here, a signature consists of a list of MuPAD domains, which represent the domains of the arguments; the domain of the result is not included in this signature). When such a function is called as f(a,b,c), it looks up the list of the domains of its arguments a, b, and c (as returned by domtype), tries to match them with the available signatures, and chooses accordingly the appropriate implementation.
-
This is a new library. It has been already used quite extensively, but all the aspects of its semantic are not yet completely fixed. The long term goal is to use it as a complete and systematic replacement of the current conversion mechanism of MuPAD, and in particular to have operators::overloaded::convertExplicit replace the standard convert function. Feedback is particularly welcome.
declareDomain – declaration of a domain
operators::overloaded::declareDomain(domain F)
Declares a new domain for which conversions might be declared.
declareConversion – declaration of a new conversion
operators::overloaded::declareConversion(domain F, domain G, function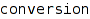 
, <opt>, 
)
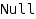Declares a new conversion from the domain F to the domain G implemented by conversion. The optional parameter opt can be either Explicit, to declare an explicit conversion, or describe the weight of the conversion. This weight can be a positive (non-negative?) rational (real?) number, or one of the predefined weights Default or Facade. Until proper weight scales are proposed, we strongly recommend to only use those predefined weights.
The weight Facade should be used when the conversion represents the inclusion of a system domain (say for example DOM_INT) into a facade domain (say Dom::Integer); in this case, conversion should be the identity id.
conversion should be a function taking an element of the domain F, and returning an element of the domain G (note that, for a facade domain G, the domain of an element of G may differ from G). If the conversion cannot be done, an error should be raised.
If a different conversion already exists from F to G, the former conversion is silently overwritten.
convert – conversion of an object
operators::overloaded::convert(object, MuPAD domain G)
Converts object into the domain G using only implicit conversions, if this is possible; otherwise, returns FAIL. In the case where G is a facade domain, the domain of the result may differ from G.
convertExplicit – explicit conversion of an object
operators::overloaded::convertExplicit(object, MuPAD domain G)
Similar to convert, but both implicit and explicit conversions may be applied.
This method is typically intended to be used in the implementation of the constructor new or of the method convert of a domain. See also the category Cat::UseOverloading.
conversion – conversion between domains
operators::overloaded::conversion(MuPAD domain F, MuPAD domain G)
operators::overloaded::conversion(MuPAD domain F, MuPAD domain G, <Cost>)
Returns the minimum weight conversion between F and G. The result is a list of functions [f1,...,fk] such that an element x of F can be converted into an element of G by (fk@...@f2@f1)(x). If there is no such conversion, FAIL is returned.
Same as above, but returns the cost of the conversion, or FAIL.
printConversions – summary of existing conversions
operators::overloaded::printConversions()
Outputs a quick summary of the existing conversions.
declareSignature – declaration of a new signature
operators::overloaded::declareSignature(overloaded function f, list of domains signature, function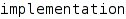 
)
Declares a new signature for the overloaded function f, implemented by implementation.
Example 1:
We start by using some predefined conversions. Here is how to convert an integer into an element of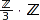 
using the canonical projection:
Z3 := Dom::IntegerMod(3):
a := operators::overloaded::convert(7, Z3)
Then, we can embed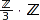 
into an algebraic extension, and do the conversion:
K := Dom::AlgebraicExtension(Z3, X^2=1):
b := operators::overloaded::convert(a, K);
domtype(b)
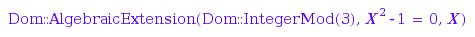
Being aware of the two basic conversions above, the system can apply them transitively:
operators::overloaded::convert(7, K)
Currently only the natural conversions between the basic MuPAD domains are predefined in the system:
operators::overloaded::printConversions()
Dom::IntegerMod(3) -> Dom::AlgebraicExtension(Dom::IntegerMod(3), X^2 - 1 = 0, X)
DOM_COMPLEX -> Dom::Complex
Dom::Real -> Dom::Complex
DOM_EXPR -> Dom::ExpressionField()
DOM_IDENT -> Dom::ExpressionField()
Dom::Complex -> Dom::ExpressionField()
DOM_FLOAT -> Dom::Float
Dom::Rational -> Dom::Float
DOM_INT -> Dom::Integer
Dom::Integer -> Dom::IntegerMod(3)
DOM_RAT -> Dom::Rational
Dom::Integer -> Dom::Rational
Dom::Float -> Dom::Real
Dom::Rational -> Dom::Real
Most of those conversions are actually trivial, since the target domains are facade domains like Dom::Integer. Furthermore, for parametrized domains like Dom::IntegerMod(3), the conversions are declared on the fly when the domains are created.
It is easy to extend the system to deal with new domains and conversions. We define the ring P of univariate polynomials over K, declare it to the conversion system, and declare the canonical embedding from the field K:
P := Dom::UnivariatePolynomial(x, K):
operators::overloaded::declareDomain(P):
operators::overloaded::declareConversion(K, P,
c -> multcoeffs(P::one, c)):
Now, we indifferently can do conversions from the integers, from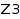 
, or from 
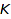into P:
c := operators::overloaded::convert(7, P);
domtype(c)
Example 2:
We define a new overloaded function myconcat which, by default, returns an unevaluated call:
myconcat := operators::overloaded
(() -> (userinfo(0, "default implementation"); hold(myconcat)(args())),
table([DOM_STRING, DOM_STRING] =
((s1,s2) -> (userinfo(0, "concatenating strings"); s1.s2)),
[DOM_LIST, DOM_LIST] =
((s1,s2) -> (userinfo(0, "concatenating lists"); s1.s2)))):
myconcat can be used indifferently to concatenate two strings or two lists:
setuserinfo(Any, 1):
setuserinfo(Graph, 0):
myconcat("bla", "ble");
myconcat([1, 2, 3], [4, 5, 6])
Info: concatenating strings
Info: concatenating lists
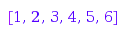
By default, an unevaluated call is returned:
myconcat(35, 73)
Info: default implementation
Let us extend the concatenation to integers, in a non standard way:
operators::overloaded::declareSignature
(myconcat,
[Dom::Integer, Dom::Integer],
(x, y) -> (userinfo(0, "concatenating integers");
text2expr(expr2text(x).expr2text(y)))):
myconcat(35, 73)
Info: concatenating integers
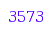
Of course, this is not very well defined, in particular if the second argument is negative!
myconcat(35, -73)
Info: concatenating integers
The point of all this is just to highlight the fact that the programmer should be very careful with the semantic of the conversions and overloaded operators he or she defines. The system does not check that they are consistent in any way; in most cases that would be impossible.
To conclude here are some examples of not-so-well defined conversions that are likely to produce problems in a larger scale environment:
operators::overloaded::declareDomain(DOM_IDENT):
operators::overloaded::declareDomain(DOM_STRING):
operators::overloaded::declareConversion(DOM_IDENT, DOM_STRING, expr2text):
myconcat(bla, "ble");
myconcat("bla", ble);
myconcat(bla, ble)
Note in particular what happens in the last computation: the system did not know how to concatenate two identifiers; so it decided to lift both identifiers into strings, and concatenate them as strings. In some cases, this behavior is perfectly acceptable (the result may, for example, live in a domain that is isomorphic to the domain of at least one of the operands), but in most cases it is not. In a future version of this library, we plan to provide means to forbid such conversions.
Background:
-
Overloaded functions shows the so-called reference effect. This is required to be able to add new signatures to an existing overloaded function. Technically, this is achieved through closures.
-
Implicit conversions should be canonical in the sense that, if there are two different ways to convert an element of a domain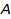 
to a domain 
(say, 
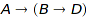, or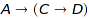 
) then the two conversions should yield mathematically equivalent results. In other words, the diagram of implicit conversions should be commutative. This does not rule out loops in the conversion diagram, and conversions are neither required to be injective nor surjective. Here are some typical good candidates for implicit conversions:
On the other hand, the conversion from the indexes of a basis of a vector space to this vector space (say, for example, from partitions to monomial symmetric functions) are usually not canonical, and in most cases should not be declared as implicit.
In most cases, those rules of thumb are enough for the programmer for deciding whether a conversion should be implicit or explicit. However a more subtle issue can arise: to be on the safe side, an implicit conversion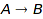 
should be a morphism for each and every overloaded function that is defined on 
.
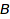Changes in MuPAD 3
New Function.