-automorphism on symmetric functions.muEC::SFA::SfAOmega – the Omega-automorphism
Compute the -automorphism on symmetric functions.
Call:
muEC::SFA::SfAOmega(sfa, <alist>)
Parameters:
|
sfa: |
any symmetric function |
|
alist: |
a list of alphabets |
Related Functions:
muEC::PART::Part2Conjugate, muEC::SYMF::SfOmega
Details:
The muEC::SFA::SfAOmega function applies the 
-automorphism to the symmetric function sfa.
This involution is defined as:
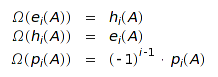
In terms of Schur functions, the involution conjugates the indexing partition.
One can apply muEC::SFA::SfAOmega solely on symmetric functions over the alphabets given in the second parameter alist.
muEC::SFA::SfAOmega( p[3,1](A1) - q*s[3](A2) );
muEC::SFA::SfAOmega( p[3,1](A1) - q*s[3](A2), [ A1 ]);
