combinat::yamanouchi – Yamanouchi words
The library combinat::yamanouchi provides functions for counting, generating, and manipulating Yamanouchi words.
→ Examples
Categories
Cat::CombinatorialClass
Details:
-
A right (respectively left) Yamanouchi word on a completely ordered alphabet, for instance [1,2,...,n], is a word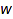 
such that any right (respectively left) factor of 
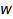contains more entries 
than 
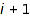. For example, the word [2, 3, 2, 2, 1, 3, 1, 2, 1, 1] is a right Yamanouchi one.
-
The evaluation of a word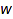 
encodes the number of occurrences of each letter of 
. In the case of Yamanouchi words, the evaluation is a partition. For example, the word [2, 3, 2, 2, 1, 3, 1, 2, 1, 1] has evaluation [4, 4, 2].
-
Yamanouchi words can be useful in the computation of Littlewood-Richardson coefficients 
. According to the Littlewood-Richardson rule, 
is the number of skew tableaux of shape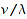 
and evaluation 
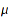, whose row readings are Yamanouchi words.
Entries
|
"domtype"
|
The MuPAD domain used to represent Yamanouchi words: DOM_LIST
|
isA – tests if an object is a Yamanouchi word
combinat::yamanouchi::isA(word w, <<Left>, <Right>>)
Returns TRUE if w is a Yamanouchi word. By default, w will be tested as a right Yamanouchi word.
list – lists Yamanouchi words
combinat::yamanouchi::list(partition p, <<Left>, <Right>>)
Returns the list of all Yamanouchi words on the alphabet [1,2,...,n] whose evaluation is p.
By default, this function returns right Yamanouchi words.
fromTableau – Yamanouchi words from standard Young tableaux
combinat::yamanouchi::fromTableau(standard tableau t, <<Left>, <Right>>)
Returns the Yamanouchi word corresponding to the standard Young tableaux t. By default, this function returns a right Yamanouchi word.
Example 1:
combinat::yamanouchi::isA([1, 2, 2, 1, 1])
combinat::yamanouchi::isA([1, 2, 2, 1, 1], Left)
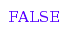
There are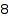 
Yamanouchi words of evaluation p = [2, 2, 2]:
combinat::yamanouchi::list([2, 2, 1])
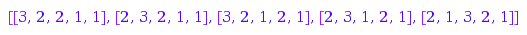
Left Yamanouchi words are obtained by just reverting right ones:
combinat::yamanouchi::list([2, 2, 1], Left)
Changes in MuPAD 3.2
New Function.