Let 
be the number of permutations of n symbols that have exactly k cycles. Then combinat::stirling1(n,k) computes 
.
Let 
be the Stirling number of the first kind, then we have:
.
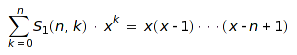combinat::stirling1 – Stirling numbers of the first kind
combinat::stirling1(n,k) computes the Stirling numbers of the first kind.
Call:
combinat::stirling1(n, k)
Parameters:
|
n, k: |
nonnegative integers |
Return Value:
an integer.
See Also:
J.J. Rotman, An Introduction to the Theory of Groups, 3rd Edition, Wm. C. Brown Publishers, Dubuque, 1988
Details:
Let be the number of permutations of n symbols that have exactly k cycles. Then combinat::stirling1(n,k) computes .
Let be the Stirling number of the first kind, then we have:
.
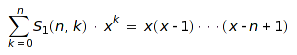Let us have a look what's the result of 
written as a sum.
expand(x*(x-1)*(x-2)*(x-3)*(x-4)*(x-5))
Now let us “prove” the formula mentioned in the “Details” section by calculating the proper Stirling numbers:
combinat::stirling1(6,1);
combinat::stirling1(6,2);
combinat::stirling1(6,3);
combinat::stirling1(6,4);
combinat::stirling1(6,5);
combinat::stirling1(6,6)
combinat::stirling1(3,-1)
Error: Arguments must be nonnegative integers. [combinat::stirling1]