combinat::parkingFunctions – parking functions
combinat::parkingFunctions is a combinatorial class that provides functions for counting, generating, and manipulating parking functions.
→ Examples
Categories
Cat::CombinatorialClass
Details:
Entries
|
"domtype"
|
The MuPAD domain used to represent parking functions: DOM_LIST
|
isA – tests if an object is a parking function
combinat::parkingFunctions::isA(word w)
Returns TRUE if w is a parking function.
list – list of parking functions
combinat::parkingFunctions::list(list p)
combinat::parkingFunctions::list(nonnegative integer n)
Returns the list of all the parking functions having the same evaluation as p (in other words, returns the list of the permutations of p if p is a parking function, and the empty list otherwise).
Returns the list of all parking functions of size n.
nonDecreasing – list of the non-decreasing parking functions
combinat::parkingFunctions::nonDecreasing(nonnegative integer n)
Returns the list of all non-decreasing parking functions of size n.
word2Parking – transforms a word into a parking function
combinat::parkingFunctions::word2Parking(word w)
Returns the parkized word of w.
breaks – breaks of a parking function
combinat::parkingFunctions::breaks(list p)
Returns the breaks of p. It is the set of integers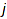 
such that the number of numbers in p smaller than or equal to 
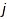is exactly 
.
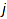prime – list of prime parking functions
combinat::parkingFunctions::prime(nonnegative integer n)
Returns the list of prime parking functions of size n, that is parking functions with no break point except n.
type – type of a parking function
combinat::parkingFunctions::type(list p)
Returns the composition associated with the breaks of p.
fromType – parking functions of a given type
combinat::parkingFunctions::fromType(list c)
Returns the parking functions of type c.
Example 1:
combinat::parkingFunctions::isA([3, 2, 5, 5, 1, 1])
combinat::parkingFunctions::isA([3, 5, 5, 1, 1])
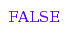
combinat::parkingFunctions::list([1, 1, 3])
There are 
parking functions with three letters.
combinat::parkingFunctions::list(3)
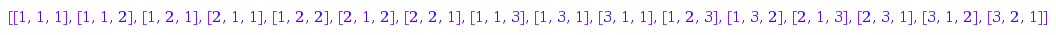
combinat::parkingFunctions::nonDecreasing(3)
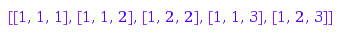
combinat::parkingFunctions::nonDecreasing(4)
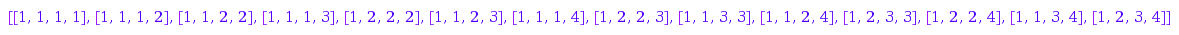
Example 2:
combinat::parkingFunctions::word2Parking([3, 5, 3, 1])
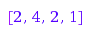
combinat::parkingFunctions::word2Parking([6, 5, 6, 9, 3, 1, 6, 6, 7])
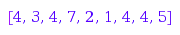
Example 3:
combinat::parkingFunctions::breaks([3, 1, 2, 2, 6, 5])
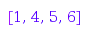
combinat::parkingFunctions::breaks([3, 1, 2, 2, 6, 5, 5])
The type of a parking function is the descent composition associated with its breaks:
combinat::parkingFunctions::type([3, 1, 2, 2, 6, 5])
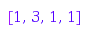
combinat::parkingFunctions::type([3, 1, 2, 2, 6, 5, 5])
combinat::parkingFunctions::prime(3)
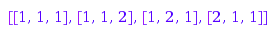
By definition, the prime parking functions have exactly one break:
map(combinat::parkingFunctions::prime(3), combinat::parkingFunctions::breaks)
select(combinat::parkingFunctions(3), z ->
combinat::parkingFunctions::breaks(z) = [3])
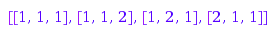
The type of a parking function is computed as
combinat::parkingFunctions::fromType([3, 1])
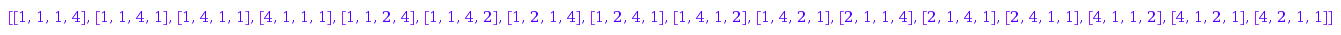
as one can check with
select(combinat::parkingFunctions(4), z -> combinat::parkingFunctions::type(z)
= [3, 1])
on the set 
such that its sorted word 
satisfies 
.
, it is possible to define a notion of parkization 
, a parking function that coincides with 
when 
is a word without repetition (see combinat::words). For 
on 
, let us define 
If 
, then 
is a parking function and the algorithm terminates, returning 
. Otherwise, let 
be the word obtained by decrementing all the elements of 
greater than 
. Then 
. Since 
is smaller than 
in the lexicographic order, the algorithm terminates and always returns a parking function.