combinat::linearExtensions – linear extensions (topological sortings) of DAGs or posets
The library combinat::linearExtensions provides functions for counting, generating, and manipulating linear extensions of directed acyclic graphs (DAGs) and in particular partially ordered sets (posets).
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass
Axioms
Ax::systemRep
Related Domains:
Graph
Details:
Entries
isA – check for linear extensions
combinat::linearExtensions::isA(list l, <directed graph g>)
Returns whether the list l is a linear extension. If g is given, returns whether the list l is a linear extension of the directed graph g.
count – number of linear extensions
combinat::linearExtensions::count(directed graph g)
Returns the number of linear extensions of the directed graph g.
generator – generator for linear extensions
combinat::linearExtensions::generator(directed graph g, <vertex order order>)
Returns a generator for the linear extensions of the directed graph g, in lexicographic order w.r.t. order.
list – list of the linear extensions
combinat::linearExtensions::list(directed graph g, <vertex order order>)
Returns the list of the linear extensions of the directed graph g, in lexicographic order w.r.t. order.
first – first linear extension
combinat::linearExtensions::first(directed graph g, <vertex order order>)
Returns the first linear extension of g, in lexicographic order w.r.t. order, or FAIL if there is none.
Next – next linear extension
combinat::linearExtensions::Next(linear extension l, directed graph g, <vertex order order>)
Returns the next linear extension of the directed graph g, in lexicographic order w.r.t. order, or FAIL if there is none.
Example 1:
Let gr be the directed graph whose edges are 
and 
:
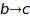gr := Graph([a, b, c], [[a, c], [b, c]], Directed)
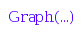
gr has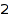 
linear extensions:
combinat::linearExtensions::count(gr)
Here is the list:
combinat::linearExtensions::list(gr)
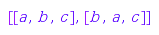
You can use the function combinat::linearExtensions::first to get the “first” linear extension a graph:
combinat::linearExtensions::first(gr)
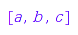
Using combinat::linearExtensions::Next, you can calculate the “next” next linear extension. This function takes as argument the linear extension relative to which you want the next one:
combinat::linearExtensions::Next([a, b, c], gr)
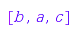
combinat::linearExtensions::Next returns FAIL when the input is the last linear extension:
combinat::linearExtensions::Next([b, a, c], gr)
When you want to run through the linear extensions of a graph, you can generate them one by one to save memory:
gr := Graph([a, b, c, d], [[a, c], [b, c], [b, d]], Directed):
g := combinat::linearExtensions::generator(gr):
g(); g(); g(); g(); g(); g();
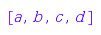
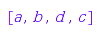
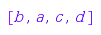
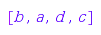
One can check that these are actually linear extensions of gr:
combinat::linearExtensions::isA([a, b, d, c], gr)
But [c, a, b, d] is not because there is an arrow [a, c] whereas a is after c:
combinat::linearExtensions::isA([c, a, b, d], gr)
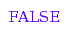
Background:
be a directed graph. A linear extension 
of 
is a total ordering 
of the vertices of 
such that 
for all edges 
of 
. There exists such a linear extension if, and only if, 
is a DAG (directed acyclic graph), that is if 
contains no cycle 
Linear extensions are also called topological sortings.
is stored as an element of the domain Graph. Linear extensions are stored as lists of vertices. The definition above rewrites as: the list L is a linear extension of G if for any edge [a,b] of G the vertex a appears before b in L.
