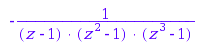combinat::integerVectorsWeighted – weighted integer vectors
The library combinat::integerVectorsWeighted provides functions for counting, generating, and manipulating weighted integer vectors.
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass, Cat::FacadeDomain(DOM_LIST)
Categories
Cat::CombinatorialClass, Cat::FacadeDomain(DOM_LIST)
See Also:
combinat::integerVectors
Details:
-
Let w be a vector of weights, ie. a list of k positive integers, and let n be a nonnegative integer. A w-weighted integer vector of sum n is a list v of k nonnegative integers such that
.
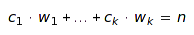For example, [1,2,0] is a [3,1,1]-weighted integer vector of sum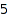 
.
-
If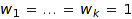 
, then a w-weighted integer vector of sum n is an integer vector of sum n; we suggest to use the much faster combinat::integerVectors library in this case.
-
If 
are variables with degree given by 
then a w-weighted integer vector of sum n is the exponent vector of a monomial of total degree n in those variables.
Entries
|
"domtype"
|
The MuPAD domain used to represent weighted integer vectors: DOM_LIST
|
count – number of weighted integer vectors
combinat::integerVectorsWeighted::count(nonnegative integer n, weight vector w)
Returns the number of w-weighted integer vectors of sum n.
list – list of the weighted integer vectors
combinat::integerVectorsWeighted::list(nonnegative integer n, weight vector w)
Returns the list of the w-weighted integer vectors of sum n.
generator – generator for weighted integer vectors
combinat::integerVectorsWeighted::generator(nonnegative integer n, weight vector w)
Returns a generator for the w-weighted integer vectors of sum n.
generatingSeries – generating series for weighted integer vectors
combinat::integerVectorsWeighted::generatingSeries(weight vector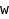 
, <indeterminate 
>)
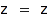Returns the generating series in z for the w-weighted integer vectors by sum.
Example 1:
There are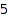 
[3,1,2]-weighted integer vectors of sum 
:
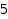combinat::integerVectorsWeighted::count(5, [3,1,2])
Here is the list:
combinat::integerVectorsWeighted::list(5, [3,1,2])
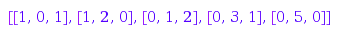
Finally, this is the generating series for the [3,1,2]-weighted integer vectors:
combinat::integerVectorsWeighted::generatingSeries([3,1,2]);
series(%,z)
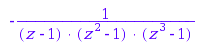
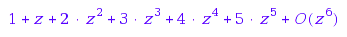
Example 2:
We search for all the ways to pay a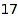 
cents postal fee using stamps of 
, 
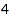, and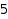 
cents:
combinat::integerVectorsWeighted(17,[3,4,5]);
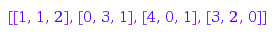
Where [1,1,2] means that we need one stamp of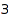 
cents, another of 
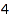and two of 
.
Another approach is to look for the partitions of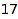 
including only 
, 
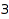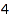, and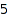 
. This is easily done by:
combinat::partitions::list(17,MinPart=3,MaxPart=5);
Background:
This library uses a crude backtrack algorithm with simple heuristics; this can be slow!