combinat::integerVectorsOfLength – integer vectors of fixed length
combinat::integerVectorsOfLength(k) creates a combinatorial class for the integer vectors of length k.
→ Examples
Categories
Cat::GradedCombinatorialClass, Cat::FacadeDomain(combinat::integerVectors)
See Also:
combinat::integerVectors
Details:
-
An integer vector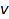 
of sum 
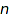and length 
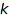is a list of 
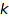nonnegative integers which sum up to 
.
-
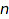combinat::integerVectorsOfLength(k) represents the graded combinatorial class of integer vectors of length k, where the size of a vector is its sum.
-
This class is typically used to represent the class of monomials in k variables, graded by degree.
-
Most functions for counting and generating accept the following optional constraints on the integer vectors: MinPart, MaxPart, Inner, Outer, MinSlope, and MaxSlope. Cf. example 2, and see combinat::integerVectors and Cat::IntegerListsLexClass for details.
isA – membership testing
combinat::integerVectorsOfLength::isA(object obj, <nonnegative integer n>)
Returns TRUE if obj is an integer vector of length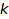 
(and, if specified, of sum n).
list – list the integer vectors
combinat::integerVectorsOfLength::list(object obj, nonnegative integer n, <constraints>)
Returns the list of integer vectors of length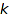 
and sum n satisfying constraints.
generator – generator for integer vectors
combinat::integerVectorsOfLength::generator(object obj, nonnegative integer n, <constraints>)
Returns a generator for the integer vectors of length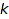 
and sum n satisfying constraints.
count – number of integer vectors
combinat::integerVectorsOfLength::count(object obj, nonnegative integer n, <constraints>)
Returns the number of integer vectors of length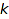 
and sum n satisfying constraints.
Example 1:
We create the combinatorial class of integer vectors of length 3:
vectors := combinat::integerVectorsOfLength(3):
There are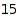 
such integer vectors of sum 
:
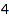vectors::count(4)
Here is the list:
vectors::list(4)
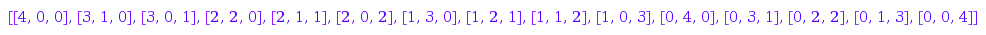
Those vectors can be identified with the following monomials in three variables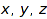 
:
vectorToMonomial := vector -> _mult(op(zip([x,y,z], vector, _power))):
map(vectors::list(4), vectorToMonomial)
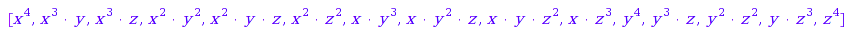
Example 2:
The usual options MinPart, MaxPart, Inner, Outer, MinSlope, and MaxSlope can be used to specify further constraints on the integer vectors. Here, we use them to obtain all the monomials of degree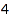 
which are divisible by 
:
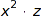map(vectors::list(4, Inner=[2,0,1]), vectorToMonomial)
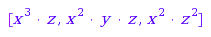
Changes in MuPAD 4.0
New Function.