combinat::integerMatrices – integer matrices
The library combinat::integerMatrices provides functions for counting, generating, and manipulating integer matrices of fixed row and column sum.
→ Examples
Superdomain
Dom::BaseDomain
Categories
Cat::CombinatorialClass
Axioms
Ax::systemRep
Related Domains:
combinat::integerVectors
Details:
Entries
|
"domtype"
|
The MuPAD domain used to represent integer matrices: DOM_LIST
|
isA – check if an object is an integer matrix
combinat::integerMatrices::isA(any type obj, <nonnegative integer c, nonnegative integer l, nonnegative integer minpart, nonnegative integer maxpart>)
Returns TRUE is obj is an integer matrix. If some of the optional arguments c, l, minpart, maxpart are given, it also checks for these extra conditions.
nrows – number of rows of an integer matrix
combinat::integerMatrices::nrows(integer matrix m)
Returns the number of rows of the integer matrix m.
ncols – number of columns of an integer matrix
combinat::integerMatrices::ncols(integer matrix m)
Returns the number of columns of the integer matrix m.
rowSums – row sums of an integer matrix
combinat::integerMatrices::rowSums(integer matrix m)
Returns the row sums of the integer matrix m.
columnSums – column sums of an integer matrix
combinat::integerMatrices::columnSums(integer matrix m)
Returns the column sums of the integer matrix m.
isSquare – "is square" predicate
combinat::integerMatrices::isSquare(integer matrix m)
Returns whether m is a square matrix.
count – number of integer matrices
combinat::integerMatrices::count(nonnegative integer c, nonnegative integer l, <nonnegative integer minpart, nonnegative integer maxpart>)
Returns the number of integer matrices of row sum c and column sum l where the sum of elements in c is equal to the sum of elements in l. If given, minpart and maxpart bound the entries of the matrices in the result.
generator – generator for integer matrices
combinat::integerMatrices::generator(nonnegative integer c, nonnegative integer l, <nonnegative integer minpart, nonnegative integer maxpart>)
Returns a generator for the integer matrices of row sum c and column sum l where the sum of elements in c is equal to the sum of elements in l. If given, minpart and maxpart bound the entries of the matrices in the result.
list – list of integer matrices
combinat::integerMatrices::list(nonnegative integer c, nonnegative integer l, <nonnegative integer minpart, nonnegative integer maxpart>)
Returns the list of the integer matrices of row sum c and column sum l where the sum of elements in c is equal to the sum of elements in l. If given, minpart and maxpart bound the entries of the matrices in the result.
standard – standardised permutation of a matrix
combinat::integerMatrices::standard(integer matrix 
)
Returns the standardized permutation of the integer matrix m. An integer matrix of row sum 
and column sum 
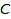can be considered as an element of a coset in the double quotient 
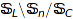where 
is the symmetric group and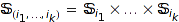 
. The standardised permutation of the integer matrix m is defined as the shortest permutation of the double coset associated to m. See NonCommutative Symmetric Functions IV: Free Quasi-Symmetric Functions and Related Algebras, G. Duchamp, F. Hivert and J.-Y. Thibon, International Journal of Algebra and Computation, Vol. 12, No. 5 (2002) 671-717.
fromStandard – matrix from its standardised permutation
combinat::integerMatrices::fromStandard(permutation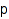 
, <nonnegative integer columnsum, nonnegative integer rowsum>)
Inverse of the standard function, it returns an integer matrix m related to the permutation p and verifying the row and column conditions. If no columnsum or rowsum are given, the smallest matrix is computed.
transpose – transposition of an integer matrix
combinat::integerMatrices::transpose(integer matrix m)
Returns the transpose of m.
With this data representation, there is no way to make a difference between a 
and 
matrix. So, in the special case of matrices with 
rows or 
lines, transpose is not involutive.
printPretty – graphic representation of a matrix
combinat::integerMatrices::printPretty(integer matrix m)
Returns a graphic representation of the matrix as rows of boxes filled with the entries of m.
printCompact – graphic representation of a skew partition
combinat::integerMatrices::printCompact(integer matrix m)
Same as above, but in a more compact way, where only the entries of m appear.
Example 1:
There are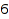 
integer matrices of column sum 
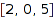and row sum 
:
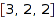combinat::integerMatrices::count([2,0,5],[3,2,2])
Here is the list:
combinat::integerMatrices::list([2,0,5],[3,2,2])
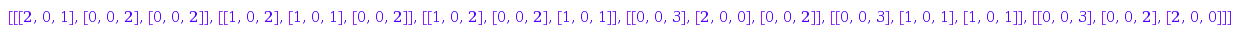
Here is a graphic representation of the list:
map(combinat::integerMatrices::list([2,0,5],[3,2,2]),
combinat::integerMatrices::printPretty)
-- +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ --
| | 2 | 0 | 1 | | 1 | 0 | 2 | | 1 | 0 | 2 | | 0 | 0 | 3 | | 0 | 0 | 3 | | 0 | 0 | 3 | |
| +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ |
| | 0 | 0 | 2 |, | 1 | 0 | 1 |, | 0 | 0 | 2 |, | 2 | 0 | 0 |, | 1 | 0 | 1 |, | 0 | 0 | 2 | |
| +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ |
| | 0 | 0 | 2 | | 0 | 0 | 2 | | 1 | 0 | 1 | | 0 | 0 | 2 | | 1 | 0 | 1 | | 2 | 0 | 0 | |
-- +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ +---+---+---+ --
Here is a more compact graphic representation of the same list:
map(combinat::integerMatrices::list([2,0,5],[3,2,2]),
combinat::integerMatrices::printCompact)
-- |2|0|1| |1|0|2| |1|0|2| |0|0|3| |0|0|3| |0|0|3| --
| |0|0|2|, |1|0|1|, |0|0|2|, |2|0|0|, |1|0|1|, |0|0|2| |
-- |0|0|2| |0|0|2| |1|0|1| |0|0|2| |1|0|1| |2|0|0| --
Among these matrices, only three have entries bounded between 0 and 2:
combinat::integerMatrices::count([2, 0, 5], [3, 2, 2], 0, 2)
Here is the list:
combinat::integerMatrices::list([2, 0, 5], [3, 2, 2], 0, 2)
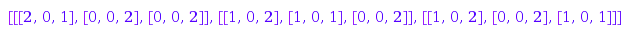
If you want to run through the integer matrices verifying some row and column sum conditions you can generate them one by one to save memory:
g := combinat::integerMatrices::generator([2,0,5],[3,2,2]):
g(); g(); g(); g(); g(); g(); g();
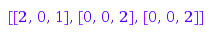
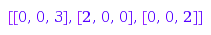
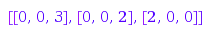
Typically, this would be used as follows:
g := combinat::integerMatrices::generator([2,0,5],[3,2,2]):
while (p := g()) <> FAIL do print(p): end:
[[2, 0, 1], [0, 0, 2], [0, 0, 2]]
[[1, 0, 2], [1, 0, 1], [0, 0, 2]]
[[1, 0, 2], [0, 0, 2], [1, 0, 1]]
[[0, 0, 3], [2, 0, 0], [0, 0, 2]]
[[0, 0, 3], [1, 0, 1], [1, 0, 1]]
[[0, 0, 3], [0, 0, 2], [2, 0, 0]]
Example 2:
In this example we check the type of some matrices. All the following tests return TRUE:
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]]);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5]);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5], [3,2,2]);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5], [3,2,2], 0);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5], [3,2,2], 0, 2);
Obviously the entries of the vector [2,0,5] are the sums of the rows of the matrix, and the entries of [3,2,2] are the sums of the columns.
combinat::integerMatrices::rowSums([[2,0,1], [0,0,2], [0,0,2]]);
combinat::integerMatrices::columnSums([[2,0,1], [0,0,2], [0,0,2]]);
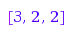
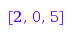
And here are some examples that return either FALSE or an error.
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[4,0,5]);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5], [3,2,2], 1);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[2,0,5], [3,2,2], 0, 1);
combinat::integerMatrices::isA([[2,0,1], [0,0,2], [0,0,2]],
[4,0,5], [3,2,2]);
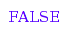
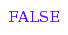
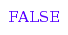
Error: Sum mismatch : [4, 0, 5] and [3, 2, 2] [combinat::integerMatrices::isA]
Example 3:
To compute the standardised permutation of the matrix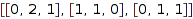 
, the MuPAD command is:
combinat::integerMatrices::standard([[0,2,1],[1,1,0],[0,1,1]])
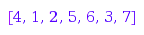
The next integer matrix gives the same standardised permutation:
combinat::integerMatrices::standard([[0,2,1],[1,2,1]])
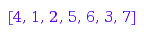
This integer matrix is the one computed by the fromStandard function when there is no more arguments than the permutation:
combinat::integerMatrices::fromStandard([4,1,2,5,6,3,7])
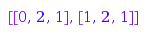
It is possible to recover other matrices with the same standardised permutation by giving row sum and column sum conditions:
combinat::integerMatrices::fromStandard([4,1,2,5,6,3,7],
[3,2,2], [3,2,2])
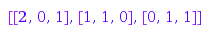
Example 4:
We transpose a little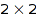 
matrix:
combinat::integerMatrices::transpose([[1, 2], [3, 4]])
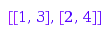
Note that when transposing a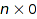 
matrix, we lose the information about the number of rows:
combinat::integerMatrices::transpose([[], [], []])
This is the only case where combinat::integerMatrices::transpose is not involutive:
combinat::integerMatrices::transpose(
combinat::integerMatrices::transpose([[], [], []]))
Background:
Except for the trivial cases, counting is done by brute force generation.
with column sums 
and row sums 
where 
is equal to 
, is a 
matrix 
such that 
, for all 
and 
, for all 
.
, 
, or 
, matrices. Unless the number of columns is provided from the context, the convention is to consider [] as the 
matrix.