. Each expression has the property that it is generated by a list of complex numbers (or a list of polynoms in future versions) 
and for all i lesser than the length of 
, and j lesser than the length of the guessed sequence, 
.combinat::guess – guessing sequences
A guessed sequence is a list of expressions . Each expression has the property that it is generated by a list of complex numbers (or a list of polynoms in future versions) and for all i lesser than the length of , and j lesser than the length of the guessed sequence, .
For instance an expression E is: - a rational function i.e. 
where 
and 
are two polynoms. (In fact, a Pade interpolation is used, so we can also find sequences with some strange terms, such as 
) - linear recursive i.e. Error: 'expression' expected [line 2, col 33]
- a sum of guessed sequence, such as: 
- a product of guessed sequence, such as: 
Entries
|
"Void" |
This is the guessed sequence corresponding tu an unguessed sequence: the list contains no element. |
term – term constructor
combinat::guess::term(integer degree)
Returns the counting function corresponding to the generating series 
.
new, func_call – guessed sequence constructor
combinat::guess::new(Type::ListOf(Type::Complex) Error: Unexpected 'identifier' [line 2, col 37]
, Method=DOM_TABLE Error: ')' expected [line 2, col 26]
, Index=Type::ListOf(DOM_IDENT) Error: Unexpected 'identifier' [line 2, col 36]
, Next=DOM_IDENT Error: Unexpected 'identifier' [line 2, col 37]
, Leaf=DOM_IDENT Error: Unexpected 'identifier' [line 2, col 36]
, OutPut=Type::Integer Error: Unexpected 'of' [line 2, col 35]
)
combinat::guess::new(combinat::guess Error: Unexpected 'identifier' [line 2, col 38]
, Type::Integer Error: Unexpected 'identifier' [line 2, col 36]
, Type::Integer Error: Unexpected 'identifier' [line 2, col 36]
)
Returns less than OutPut (or exactly OutPut) formulas describing a sequence which first terms are the one given. Only the first terms are necessary, the other parameters have default values. The parameters of a method are: MaxDepth which controls how many time... MinPoints which decides how many values are required to make a guess TestPoints which decides how many values are remembered for testing purpouses Block_Guess decides if Guess Method needs not to be run (don't toggle it!) Block_LinRec idem with LinRec (Sum and Prod automatically block it by default) Block_RatInterp idem with RatInterp Block_Sum idem with Sum Block_Prod idem with Prod
If 
is the guessed sequence, 
is the i-th term of the n-th sequence of the list of guessed sequence 
. And 
is the i-th term of the 1st sequence (same as 
).
We can try to guess [1,1,1,1,1,1]
Ones := [1,1,1,1,1,1];
Default values give(fastest result):
combinat::guess(Ones);
Now, for more results:
combinat::guess(Ones, Output = 3)
For best result:
combinat::guess(Ones, Output = 1)
And how to use a guessed sequence:
W := combinat::guess([1,1,2,6,24,120], Output = 3)
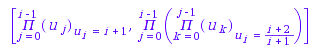
Naturally they all define n!, so the 7th term of each formula is the same:
W[1](7), W[2](7)
The parameters have default values, (read guess.mu), but other values can be used:
LinRecTest := table(TestPoints = 0):RatInterpTest := table(TestPoints = 0):
Now, there won't be any test
T := combinat::guess([0,1,1,2,3,5],LinRec = LinRecTest,RatInterp = RatInterpTest,Output = 5)
With no test too many expressions are found and they are different:
T[1](7), T[2](7), T[3](7), T[4](7), T[5](7)
if i,j,k,i1,i2... are no good names, you can do:
U := combinat::guess([0,1,1,2,3,5],LinRec = LinRecTest,RatInterp = RatInterpTest,Output = 5,Indices = [x,y,z],Next = t, Leaf = i):extop(U)[2];
RatInterp and LinRec use a "clever" Pade Interpolation, that allows unexpected values:
combinat::guess([1,23,1,1,1,1])
In fact, for Rationnal Interpolation, the formula computed is: 
, that means u(i)=1 for all i excepted i=1 and is undefined in 1. The program memorize that for i=1, u(i)=23