combinat::graphs – unlabelled graphs, an interface with Nauty
combinat::graphs is an interface with the Nauty C library for manipulating unlabelled graphs.
→ Examples
Details:
-
combinat::graphs provides a dynamic module interface with the Nauty C library for counting, generating, and manipulating unlabelled graphs.
-
All functions for counting and generating accept the following optional constraints on the graphs: Connected, C3Free, C4Free, Bipartite, Biconnected, MinDegree, MaxDegree, MinEdges, MaxEdges, whose respective meaning are self-explanatory. Furthermore, the options Quiet and GengOptions can be used to pass extra options to Nauty.
-
Unlabelled graphs are represented by a (canonical) labelled representative on the vertices  . Technically, they are stored as kernel objects; namely, they consist of MuPAD cells of type combinat::graphs whose memory parts embed a C graph data structure, as used by Nauty.
. Technically, they are stored as kernel objects; namely, they consist of MuPAD cells of type combinat::graphs whose memory parts embed a C graph data structure, as used by Nauty.
count – number of graphs
combinat::graphs::count(nonnegative integer 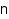 , <constraints>)
, <constraints>)
Returns the number of graphs on n vertices satisfying constraints.
list – list of graphs
combinat::graphs::list(nonnegative integer 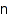 , <constraints>)
, <constraints>)
Returns the list of the graphs on n vertices satisfying constraints.
size – number of vertices of a graph
combinat::graphs::size(dom g)
Returns the number of vertices of g.
getVertices – vertices of a graph
combinat::graphs::getVertices(dom g)
Returns the list of the vertices of g.
getEdges – edges of a graph
combinat::graphs::getEdges(dom g)
Returns the list of the edges of g.
getEdgeNumber – number of edges of a graph
combinat::graphs::getEdgeNumber(dom g)
Returns the number of edges of g.
outDegree – out degree
combinat::graphs::outDegree(dom g, vertex i)
Returns the out degree of the vertex i of g.
outDegrees – out degrees
combinat::graphs::outDegrees(dom g)
Returns the list of the out degrees of the vertices of g.
addEdges – adding edges
combinat::graphs::addEdges(dom g, list of edges edges)
Returns a copy of g with the edges in edges added.
removeEdges – removing edges
combinat::graphs::removeEdges(dom g, list of edges edges)
Returns a copy of g with the edges in edges removed.
relabel – relabelling of the vertices
combinat::graphs::relabel(dom g, standard permutation p)
Returns a copy of g, with the vertices relabelled according to the permutation p; that is, the node i of the new graph corresponds to the node p[i] of g.
sublabel – induced subgraph
combinat::graphs::sublabel(dom g, list of vertices p)
Returns an isomorphic copy of the induced subgraph of g on the vertices p. The node i of the new graph corresponds to the node p[i] of g.
When p is a standard permutation, this is equivalent to relabel above.
straighten – canonical representative
combinat::graphs::straighten(dom g)
Returns a canonical isomorphic copy of g.
removeIsolatedVertices – removing isolated vertices
combinat::graphs::removeIsolatedVertices(dom g)
Returns an isomorphic copy of g with the isolated vertices removed.
directSum – direct sum of two graphs
combinat::graphs::directSum(dom g, dom h)
Returns the direct sum of g and h; it is obtained by a copy of g, with the vertices relabelled according to some permutation p; that is, the node i of the new graph corresponds to the node p[i] of g.
Example 1:
Here is the list of all 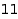 unlabelled unoriented loopfree simple graphs on
unlabelled unoriented loopfree simple graphs on 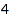 vertices:
vertices:
combinat::graphs::list(4)
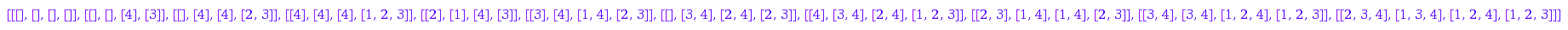
Let's take the 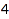 -th one:
-th one:
g := combinat::graphs(4)[4]

It is displayed using adjacency lists: for each vertex, the list of its neighbors is given. Some basic accessors, named as in the Graph library, allow to retrieve information from the graph:
combinat::graphs::getVertices(g)
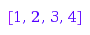
combinat::graphs::getEdgeNumber(g)

combinat::graphs::getEdges(g)
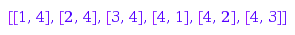
combinat::graphs::outDegrees(g)
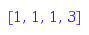
Example 2:
Let us take two small graphs:
lg := combinat::graphs::list(5):
g1 := lg[10];
g2 := lg[25];
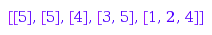

The direct sum of g1 and g2 is the graph
gd := combinat::graphs::directSum(g1, g2)
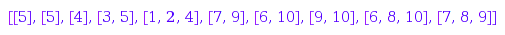
The canonical labelling of gd is
gc := combinat::graphs::straighten(gd)
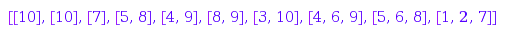
One can check indeed that a relabelling of gd gives gc
gc := combinat::graphs::relabel(gd, [1,2,3,6,7,8,4,9,10,5]);
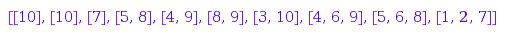
Changes in MuPAD 3.1
New Function.
![]() . Technically, they are stored as kernel objects; namely, they consist of MuPAD cells of type combinat::graphs whose memory parts embed a C graph data structure, as used by Nauty.
. Technically, they are stored as kernel objects; namely, they consist of MuPAD cells of type combinat::graphs whose memory parts embed a C graph data structure, as used by Nauty.