combinat::bell – Bell numbers
combinat::bell(n) computes the n-th Bell number.
→ Examples
Calls:
combinat::bell(n)
combinat::bell(expression)
Parameters:
|
n:
|
nonnegative integer
|
|
expression:
|
An expression of type Type::Arithmetical which must be a nonnegative integer if it is a number.
|
Return Value:
A positive integer value if n was a nonnegative integer. Otherwise combinat::bell returns the unevaluated function call.
Details:
-
The n-th Bell number is defined by the exponential generating function:
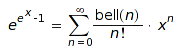
Often another definition is used. The n-th Bell number is the number of different ways of partitioning the set 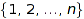 into disjoint nonempty subsets, and
into disjoint nonempty subsets, and 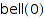 is defined to be 1.
is defined to be 1.
-
Bell numbers are computed using the formula:
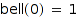
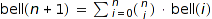 for
for 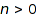
Example 1:
Example 2:
If one uses a wrong argument, an error message is returned.
combinat::bell(3.4)
Error: Nonnegative integer expected [combinat::bell]
Example 3:
It can be useful to return the unevaluated function call.
a := combinat::bell(x);
x := 4;
a ;
delete(a);


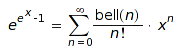
![]() into disjoint nonempty subsets, and
into disjoint nonempty subsets, and ![]() is defined to be 1.
is defined to be 1.![]()
![]() for
for ![]()