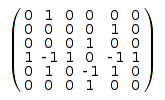combinat::alternatingSignMatrices – alternating sign matrices
combinat::alternatingSignMatrices represents the combinatorial class of alternating sign matrices.
Categories
Cat::GradedCombinatorialClass, Cat::FacadeDomain(matrix)
Details:
An alternating sign matrix of size 
is a 
square matrix of 
's, 
's, and 
's such that the non-zero entries of each row begin and end with 
's and alternate in sign, and the non-zero entries of each column have the same property. Here is a typical alternating sign matrix of size 
:
These matrices form a natural generalization of permutations, and appear in many different contexts like statistical mechanics.
Method count is inherited from Cat::GradedCombinatorialClass.
Method generator is inherited from Cat::GradedCombinatorialClass.
Method list is inherited from Cat::GradedCombinatorialClass.
We start by counting the number of alternating sign matrices; this uses the classical (and hard to prove!) formula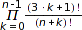 
:
combinat::alternatingSignMatrices::count(n) $ n = 0..10
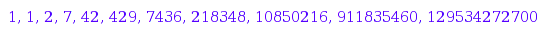
From this, we see that the first alternating sign matrix that is not a permutation matrix is of size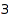 
. Here it is:
combinat::alternatingSignMatrices::list(3)
Background:
See the Wikipedia article on alternating sign matrices: http://en.wikipedia.org/wiki/Alternating_sign_matrix.
Changes in MuPAD 4.0
New Function.