given by its linear representation where 
, 
, 
, 
and 
are respectively the dimension, the alphabet, the initial vector, the transition function and the final vector.Dom::WeightedAutomaton – set of weighted automata
Dom::WeightedAutomaton(S) creates a domain for weighted automata with multiplicities in the component semi-ring S.
The domain element Dom::WeightedAutomaton(S)(n,A,i,t,f) represents the weighted automaton with multiplicities in the semi-ring given by its linear representation where , , , and are respectively the dimension, the alphabet, the initial vector, the transition function and the final vector.
Creating the Type
Dom::WeightedAutomaton(S)
WeightedAutomaton(S)(n, A, i, t, f)
Parameters:
|
S: |
a semiring, i.e., a domain of category Cat::SemiRing |
|
n: |
positive integer. |
|
A: |
list. |
|
i: |
|
|
t: |
table indexed by elements of |
|
f: |
|
Superdomain
Related Domains:
Dom::BooleanSemiRing, Dom::MaxMinSemiRing, Dom::MaxPlusSemiRing, Dom::MinMaxSemiRing, Dom::MinPlusSemiRing
Mathematical Methods
domtypeweight – data type of weights
(Dom::WeightedAutomaton(S))::domtypeweight()
The data type of weights is given.
weight – weight of a word
(Dom::WeightedAutomaton(S))::weight(dom wa, DOM_LIST u)
The weight of the word u given by a list [u1,u2,
,uk] is defined to be the product of sparse matrices i*t[u1]*t[u2]*
*t[uk]*f.
proper – proper automaton of a weighted automaton
(Dom::WeightedAutomaton(S))::proper(dom wa)
The proper automaton of a weighted automaton keeps the same behaviour with the weight 
for the empty word [].
addLetter – new letter and its transition matrix
(Dom::WeightedAutomaton(S))::addLetter(dom wa, any x, Dom::Matrix(S) Mx)
A letter x and its transition matrix Mx are added to the weighted automaton wa.
delLetter – removing a letter and its transition matrix
(Dom::WeightedAutomaton(S))::delLetter(dom wa, any x)
A letter x and its transition matrix Mx is removed from the weighted automaton wa.
addState – new state with transitions, initial and final weight
(Dom::WeightedAutomaton(S))::addState(dom wa, Dom::Matrix(S) it, Dom::Matrix(S) ot, S i, S f)
A state is added to the weighted automaton wa. It is indexed by d+1 if d is the dimension of wa. If they are given, the ingoing transitions it and the outgoing transitions ot written as a row vector and a column vector respectively, are considered just as the initial weight i and the final weight f.
delState – delete a state
(Dom::WeightedAutomaton(S))::delState(dom wa, Type::PosInt s)
The state s is removed from the weighted automaton wa.
subsTransition – insert a weight for a transition
(Dom::WeightedAutomaton(S))::subsTransition(dom wa, dom t, S w)
The weight w is put for the transitionsss t in the weighted automaton wa. If it is not given, the weight is the neutral element of S for the multiplication. If the weight is the neutral element of S for the addition, the transition t is removed.
subsInitialWeight – insert an initial weight for a state
(Dom::WeightedAutomaton(S))::subsInitialWeight(dom wa, Type::PosInt s, S w)
The initial weight w is put for the state s in the weighted automaton wa. If it is not given, the initial weight is the neutral element of S for the multiplication. If the weight is the neutral element of S for the addition, the state s becomes non-initial.
subsFinalWeight – insert a final weight for a state
(Dom::WeightedAutomaton(S))::subsFinalWeight(dom wa, Type::PosInt s, S w)
The final weight w is put for the state s in the weighted automaton wa. If it is not given, the final weight is the neutral element of S for the multiplication. If the weight is the neutral element of S for the addition, the state s becomes non-final.
dimension – dimension of a weighted automaton
(Dom::WeightedAutomaton(S))::dimension(dom wa)
The dimension of a weighted automaton is defined to be the dimension of transition matrices.
alphabet – alphabet of a weighted automaton
(Dom::WeightedAutomaton(S))::alphabet(dom wa)
The alphabet of the weighted automaton is computed.
initial – initial vector of a weighted automaton
(Dom::WeightedAutomaton(S))::initial(dom wa)
The initial vector of the weighted automaton is computed.
transition – transition matrix of a weighted automaton
(Dom::WeightedAutomaton(S))::transition(dom wa, any x)
The transition function of the weighted automaton is returned if x is not given, the transition matrix of x otherwise.
final – final vector of a weighted automaton
(Dom::WeightedAutomaton(S))::final(dom wa)
The final vector of the weighted automaton is computed.
tensor – Kronecker product of sparse matrices
(Dom::WeightedAutomaton(S))::tensor(Dom::Matrix(S) A, Dom::Matrix(S) B)
The Kronecker product of the sparse matrices A and B is computed.
mstar – Star of a sparse matrix
(Dom::WeightedAutomaton(S))::mstar(Dom::Matrix(S) A)
The star of the sparse matrix A is computed.
_plus – sum of weighted automata
(Dom::WeightedAutomaton(S))::_plus(dom 
, ...)
The sum 
of weighted automata is defined to be the weighted automaton with 
the weight of a word 
if 
is the weight of 
for the automaton 
.
This method overloads the function _plus.
_mult – Cauchy product of weighted automata
(Dom::WeightedAutomaton(S))::_mult(dom 
, ...)
The Cauchy product 
of weighted automata is defined to be the weighted automaton with the sum 
the weight of a word 
if 
is the weight of the word 
for the automaton wai for each decomposition 
.
This method overloads the function _mult.
_power – Power of a weighted automaton
(Dom::WeightedAutomaton(S))::_power(dom wa, Dom::Integer i)
The ith power 
of the weighted automaton wa.
This method overloads the function _power.
hadamard – Hadamard product of weighted automata
(Dom::WeightedAutomaton(S))::hadamard(dom 
, dom 
)
The Hadamard product of two weighted automata 
and 
is defined to be the weighted automaton with 
the weight of a word 
if 
is the weight of the word 
for the automaton 
.
shuffle – shuffle product of weighted automata
(Dom::WeightedAutomaton(S))::shuffle(dom 
, dom 
)
The shuffle product of two weighted automata 
and 
is computed with the shuffle of the rational noncommutative formal series 
and 
as behaviour if 
and 
are respectively the behaviour of 
and 
.
infiltration – infiltration product of weighted automata
(Dom::WeightedAutomaton(S))::infiltration(dom 
, dom 
)
The infiltration product of two weighted automata 
and 
is computed with the infiltration of the rational noncommutative formal series 
and 
as behaviour if 
and 
are respectively the behaviour of 
and 
.
star – star of a weighted automaton
(Dom::WeightedAutomaton(S))::star(dom wa)
The star of a weighted automaton wa with the rational noncommutative formal series 
as behaviour is returned with the star of 
(if there exists) as behaviour.
complementary – complementary of a weighted automaton
(Dom::WeightedAutomaton(S))::complementary(dom wa)
This method returns the complementary of boolean weighted automaton wa, and FAIL otherwise.
difference – difference of weighted automata
(Dom::WeightedAutomaton(S))::difference(dom 
, dom 
)
This method returns the difference of boolean weighted automata 
and 
, and FAIL otherwise.
elimination – elimination of a letter in a weighted automaton
(Dom::WeightedAutomaton(S))::elimination(dom wa, any x)
The x-removing of a weighted automaton wa produces (if there exists) a weighted automaton on the alphabet without x where the new transition matrix of a letter is computed from the product of the star of the transition matrix of x and the old transition matrix.
isComplete – checks whether a weighted automaton is complete
(Dom::WeightedAutomaton(S))::isComplete(dom wa)
This method returns TRUE if the weighted automaton wa is complete, and FALSE otherwise.
complete – computation of the complete weighted automaton
(Dom::WeightedAutomaton(S))::complete(dom wa)
This method returns the complete automaton corresponding to the weighted automaton wa.
isAccessible – checks whether a weighted automaton is accessible
(Dom::WeightedAutomaton(S))::isAccessible(dom wa, Type::PosInt q)
(Dom::WeightedAutomaton(S))::isAccessible(dom wa, Type::SetOf(Type::PosInt) s)
This method returns TRUE if the weighted automaton wa is accessible, and FALSE as well as the set of accessible states otherwise. When a second argument is given, if the state q (or the set s of states) is accessible then TRUE is returned, else FALSE.
accessible – computation of the accessible weighted automaton
(Dom::WeightedAutomaton(S))::accessible(dom wa)
This method returns the accessible automaton corresponding to the weighted automaton wa.
isCoaccessible – checks whether a weighted automaton is coaccessible
(Dom::WeightedAutomaton(S))::isCoaccessible(dom wa, Type::PosInt qt)
(Dom::WeightedAutomaton(S))::isCoaccessible(dom wa, Type::SetOf(Type::PosInt) 
)
This method returns TRUE if the weighted automaton wa is coaccessible, and FALSE as well as the set of coaccessible states otherwise. When a second argument is given, if the state q (or the set s of states) is coaccessible then TRUE is returned, else FALSE.
coaccessible – computation of the coaccessible weighted automaton
(Dom::WeightedAutomaton(S))::coaccessible(dom wa)
This method returns the coaccessible automaton corresponding to the weighted automaton wa.
trim – computation of the trimed weighted automaton
(Dom::WeightedAutomaton(S))::trim(dom wa)
This method returns the trimed automaton corresponding to the weighted automaton wa.
isDeterministic – checks whether a weighted automaton is deterministic
(Dom::WeightedAutomaton(S))::isDeterministic(dom wa)
This method returns TRUE if the weighted automaton wa is deterministic, and FALSE otherwise.
determinization – determinization of a weighted automaton
(Dom::WeightedAutomaton(S))::determinization(dom wa)
This method returns the determinization of the weighted automaton wa if it is possible, and FAIL otherwise.
minimization – minimization of a weighted automaton
(Dom::WeightedAutomaton(S))::minimization(dom wa)
This method returns the minimization of the weighted automaton wa if it is possible, and FAIL otherwise.
areEquivalent – equivalence of weighted automata
(Dom::WeightedAutomaton(S))::areEquivalent(dom 
, dom 
)
This method checks whether the weighted automata 
and 
are the same behaviour.
leftQuotient – left quotient of a weighted automaton
(Dom::WeightedAutomaton(S))::leftQuotient(dom wa, DOM_LIST u)
This method returns the left quotient of the weighted automaton wa by the word u. More precisely, the behaviour of the resulted weighted automaton is the right action of u on the behaviour of wa.
rightQuotient – right quotient of a weighted automaton
(Dom::WeightedAutomaton(S))::rightQuotient(dom wa, DOM_LIST u)
This method returns the right quotient of the weighted automaton wa by the word u. More precisely, the behaviour of the resulted weighted automaton is the left action of u on the behaviour of wa.
Conversion Methods
changeCoeffRing – conversion of a weighted automaton to a weighted automaton over another semiring
(Dom::WeightedAutomaton(S))::changeCoeffRing(dom wa, any T)
Tries to convert the weighted automaton wa into a weighted automaton over scalars of type T.
We want to work with weighted automata whose multiplicities are in the MinPlus semiring. First, we choose the weights:
T:=Dom::MinPlusSemiRing:
The domain of corresponding weighted automata is introduced:
TW:=Dom::WeightedAutomaton(T):
We need transition matrices:
TM:=Dom::Matrix(T):
Now we show how to construct a MinPlus automaton with two states over the alphabet {a,b}:
alphabet1:=[a,b]:
We describe the initial (row-)vector; there is a single initial state, namely state 1 with weight 2:
l1:=TM(1,2,[T(2),T(infinity)]);
Transition matrice for the letter a are given. For instance, the transition from the state 2 to the state 1 is valuated by 1 for the letter a:
m1[a]:=TM(2,2,[[T(0),T(1)],[T(1),T(infinity)]]);
and for the letter b:
m1[b]:=TM(2,2,[[T(infinity),T(0)],[T(1),T(1)]]);
Finally, there is the final (column-)vector with 1 et 2 as final states with weigths 0 and 1 respectively:
g1:=TM(2,1,[T(0),T(1)]);
Now we assemble the pieces and build the automaton:
wa1:=TW(2,alphabet1,l1,m1,g1);
The weight of a word is computed:
TW::weight(wa1, [a, a, b, a])
Some functionalities on weighted automata are available. We can compute the proper automaton:
TW::proper(wa1)
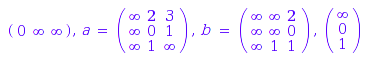
A letter with its transition matrix can be added:
TW::addLetter(wa1, c, TM(2, 2, [[T(2), T(1)], [T(3), T(2)]]))
Addition of weighted automata is possible. Then we define another MinPlus automaton:
alphabet2:=[a,c]:
l2:=TM(1,3,[T(1),T(0),T(1)]):
m2[a]:=TM(3,3,[[T(2),T(1),T(infinity)],[T(1),T(0),T(0)],[T(1),T(infinity),
T(2)]]):
m2[c]:=TM(3,3,[[T(1),T(infinity),T(0)],[T(2),T(2),T(infinity)],[T(infinity),
T(1),T(0)]]):
g2:=TM(3,1,[T(infinity),T(0),T(1)]):
wa2:=TW(3,alphabet2,l2,m2,g2);
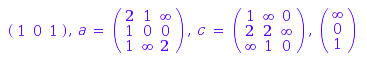
The addition returns:
wa1 + wa2
The Cauchy product of weighted automata:
wa1*wa2
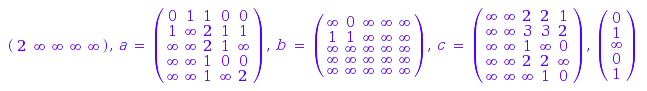
The nth power of a weighted automaton:
wa1^2
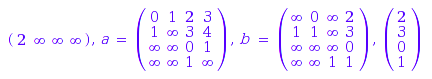
The Hadamard product:
TW::hadamard(wa1, wa2)
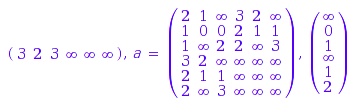
The shuffle product:
TW::shuffle(wa1, wa1)
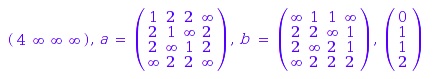
The star operation:
TW::star(wa1)
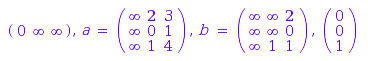
A letter can be algebraically removed giving the classical solution in the boolean case:
TW::elimination(wa1, a)
We can test if an automaton is accessible, coaccessible, or complete. Accessible, coaccessible, trimed or complete weighted automata can be computed. For instance, we construct a MinPlus automaton whose the state 2 is non-accessible:
alphabet:=[a, b]:
l:=TM(1, 2, [T(1), T(infinity)]):
m[a]:=TM(2, 2, table((1, 1) = T(1), (2, 1) = T(1))):
m[b]:=TM(2, 2, table((2, 2) = T(1))):
g:=TM(2, 1, [T(infinity), T(1)]):
wa:=TW(2, alphabet, l, m, g);
Therefore wa has only one accessible state which is 1:
TW::isAccessible(wa);
The corresponding accessible automaton is computed:
TW::accessible(wa);
The MinPlus automaton wa is non-coaccessible; the only coaccessible state is 2:
TW::isCoaccessible(wa);
The corresponding coaccessible automaton is computed:
TW::coaccessible(wa)
Non-accessible and non-coaccessible states can be removed:
TW::trim(wa)
++ ++ ++ +- -+
||, a = ++, b = ++, +- -+
++
We can check also if a weighted automaton is complete. The state 1 of the MinPlus automaton wa does not have outgoing transitions labelled by the letter b:
TW::isComplete(wa);
The corresponding complete automaton is computed:
TW::complete(wa);
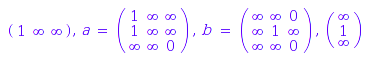
Deterministic automata can be computed. A _divide method is required for the weights of automata. Here a MinPlus automaton:
l := TM(1, 4, [T(0), T(infinity), T(infinity), T(infinity)]):
m[a] := TM(4, 4, table((1, 2) = T(3), (1, 3) = T(1))):
m[b] := TM(4, 4, table((1, 2) = T(1), (1, 3) = T(4), (2, 4) = T(1))):
g := TM(4, 1, [T(infinity), T(0), T(infinity), T(0)]):
wa := TW(4, alphabet, l, m, g);
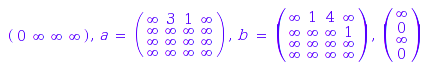
TW::determinization(wa);
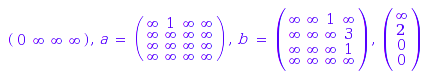
Minimal automata (in the number of states) can be computed. For instance, we choose a Z-automaton with three states:
Z:=Dom::Integer:
W:=Dom::WeightedAutomaton(Z):
M:=Dom::Matrix(Z):
alphabet:=[a, b]:
l:=M(1, 3, [2, -1, 1]):
ma:=M(3, 3, [[0, -1, 2], [1, 1, -1], [0, 0, 1]]):
mb:=M(3, 3, [[-2, 0, 0], [0, -1, 2], [0, 0, -1]]):
g:=M(3, 1, [1, -2, 0]):
aut:=W(3, alphabet, l, table(a = ma, b = mb), g);
The minimal automaton corresponding to the Z-automaton aut has two states:
W::minimization(aut)
Two Z-automata are equivalent if their behaviours are the same. We test this property:
W::areEquivalent(aut, last(1))
When the weights belong to the boolean semiring or exotic semirings, minimal deterministic automata are returned. The following MinPlus automaton wa have four states but it is not deterministic:
l := TM(1, 4, [T(0), T(infinity), T(infinity), T(infinity)]):
m[a] := TM(4, 4, table((1, 2) = T(3), (1, 3) = T(1))):
m[b] := TM(4, 4, table((1, 2) = T(1), (1, 3) = T(4), (2, 4) = T(1))):
g := TM(4, 1, [T(infinity), T(0), T(infinity), T(0)]):
wa := TW(4, alphabet, l, m, g):
The corresponding minimal deterministic automaton has three states:
TW::minimization(wa);
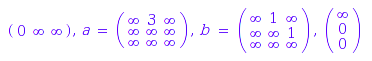
Left or right quotients can be computed:
TW::leftQuotient(wa, [a, c, b, a])
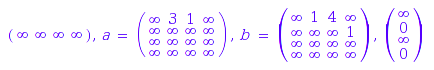
TW::rightQuotient(wa, [a, c, b, a])
+- -+
| 1, infinity, infinity, infinity |,
+- -+
+- -+
| infinity, 1, infinity, infinity |
| |
| infinity, infinity, infinity, 1 |
a = | |,
| infinity, infinity, infinity, 1 |
| |
| infinity, infinity, infinity, infinity |
+- -+
+- -+
| infinity, infinity, 1, infinity |
| |
| infinity, 1, infinity, infinity |
b = | |,
| infinity, infinity, infinity, infinity |
| |
| infinity, infinity, infinity, infinity |
+- -+
+- -+
| infinity, infinity, infinity, infinity |
| |
| infinity, 1, infinity, infinity |
c = | |,
| infinity, infinity, 1, infinity |
| |
| infinity, infinity, infinity, infinity |
+- -+
+- -+
| 5 |
| |
| infinity |
| |
| infinity |
| |
| infinity |
+- -+
Boolean operations are available. First, we construct a boolean automaton:
B:=Dom::BooleanSemiRing:
W:=Dom::WeightedAutomaton(B):
BM:=Dom::Matrix(B):
alphabet:=[a, b]:
l:=BM(1, 2, [0, 1]):
ma:=BM(2, 2, [[0, 1], [1, 1]]):
mb:=BM(2, 2, [[1, 0], [1, 1]]):
g:=BM(2, 1, [0, 1]):
wa:=W(2, alphabet, l, table(a = ma, b = mb), g)
We check whether wa is deterministic. Clearly there are two outgoing transitions labelled by the letter a from the state 2:
W::isDeterministic(wa)
The corresponding deterministic automaton is returned:
W::determinization(wa)
The complementary:
W::complementary(wa)
Difference of boolean automata is possible. We create another automaton:
I1:=BM(1, 1, [1]):
W(1, alphabet, I1, table(a = I1, b = I1), I1)
Then:
W::difference(wa, last(1))
