, that is, the domain of all the permutations of 
elements.Dom::SymmetricGroup – symmetric groups
Dom::SymmetricGroup(n) creates the symmetric group of order , that is, the domain of all the permutations of elements.
Creating the Type
Dom::SymmetricGroup(n)
Parameters:
|
n: |
positive integer |
Details:
A permutation of 
elements is a bijective mapping of the set 
onto itself.
Dom::SymmetricGroup inherits from all the methods and entries defined in its super domain Dom::PermutationGroup.
Creating Elements
Dom::SymmetricGroup(n)(l)
Parameters:
|
l: |
list or array consisting of the first |
Superdomain
Categories
Axioms
Related Domains:
Details:
The domain element Dom::SymmetricGroup(n)(l) represents the bijective mapping of the first 
positive integers that maps the integer 
to l[i], for 
.
Entries
|
"one" |
the identical mapping of the set |
Mathematical Methods
_mult – product of permutations
(Dom::SymmetricGroup(n))::_mult(dom a1, ...)
The product 
of permutations is defined to be the mapping that assigns, to every integer i between 
and 
, the integer a1(a2(...ak(i)...)).
This method overloads the function _mult.
_invert – inverse of a permutation
(Dom::SymmetricGroup(n))::_invert(dom a)
This method computes a permutation b such that a*b is the identity mapping.
This method overloads the function _invert.
func_call – function value of a permutation at a point
(Dom::SymmetricGroup(n))::func_call(dom a, integer i)
This method overloads the round brackets (...), i.e. it may be called in the form a(i).
It computes the function value of a at i, i.e., the integer that i is mapped to by the permutation a; i must be an integer between 
and 
.
cycles – cycle representation of a permutation
(Dom::SymmetricGroup(n))::cycles(dom a)
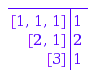
This method computes a cycle representation of a. A cycle representation is a list [orbit1, ... , orbitk]; each of the orbits is a list of integers of the form [i, a(i), a(a(i)), ...] with just as many elements such that i does not occur in it for a second time; each integer between 
and 
appears in exactly one of the orbits.
order – order of a permutation
(Dom::SymmetricGroup(n))::order(dom a)
The order of a is defined to be the least positive integer k for which 
is the identity.
inversions – number of inversions
(Dom::SymmetricGroup(n))::inversions(dom a)
This method computes the number of all pairs 
of integers for which 
but 
.
sign – sign of a permutation
(Dom::SymmetricGroup(n))::sign(dom a)
This method returns the sign of the permutation a. The sign of a permutation is defined to be 
if its number of inversions is even, and 
otherwise.
random – random permutation
(Dom::SymmetricGroup(n))::random()
This method returns a random element of the permutation group.
charactersTable – computation of the characters table
(Dom::SymmetricGroup(n))::charactersTable()
Returns the character table for the symmetric group (the computation uses SgCharTable from the Symmetrica module). The returned table has entries indexed by couples of partitions: the first coordinate corresponds to a conjugancy class and the second one to an irreductible representation.
Access Methods
allElements – return all elements of the group
(Dom::SymmetricGroup(n))::allElements()
This method returns the list of the elements of the group.
size – return the size of the group
(Dom::SymmetricGroup(n))::size()
This method returns the size of the group.
Conversion Methods
convert – conversion of an object into a permutation
(Dom::SymmetricGroup(n))::convert(any x)
This method tries to convert x into a permutation. This is only possible if x is a list or an array in which each of the integers 
through 
occurs exactly once.
convert_to – conversion of a permutation into another type
(Dom::SymmetricGroup(n))::convert_to(dom a, any T)
Tries to convert a into type T. Currently, only a conversion into a list of type DOM_LIST is possible.
expr – convert a permutation into a list
(Dom::SymmetricGroup(n))::expr(dom a)
This method returns a list such that generating a permutation from that list would result in a.
Consider the group of permutations of the first seven positive integers:
G := Dom::SymmetricGroup(7)
We create an element of G by providing the image of 
, 
, etc.:
a:=G([2,4,6,1,3,5,7])
a(3)
Computation of the characters table for the symmetric group 
:
G := Dom::SymmetricGroup(3)
t := G::charactersTable()
