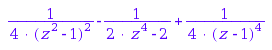In this example, we show how to manipulate invariants of the cyclic group 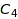 with rational coefficients:
with rational coefficients:
C4 := Dom::PermutationGroup(4, [[[1,2,3,4]]]):
IC4 := Dom::PermutationGroupInvariantRing(Dom::Rational, C4):
Given a monomial, say  , the orbit sum of
, the orbit sum of  is the sum of all the monomials in the orbit of m by the action of the group. For example, the orbit sum of
is the sum of all the monomials in the orbit of m by the action of the group. For example, the orbit sum of  under the action of
under the action of  is
is  . Such an orbit sum is stored compactly, by just keeping track of the leading monomial.
. Such an orbit sum is stored compactly, by just keeping track of the leading monomial.
Monomials themselves are represented by theirs exponent vectors; the 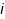 -th entry of the list being the power of the
-th entry of the list being the power of the 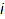 -th variable.
-th variable.
Time for an example, the following defines the orbit sum of 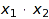 :
:
m := IC4([1, 1, 0, 0])
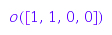
Only the leading term is displayed, but this really represents the full orbitsum of 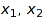 :
:
IC4::poly(m)
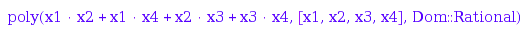
Here is the first powersum of degree 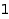 :
:
p1 := IC4([1, 0, 0, 0]);
IC4::poly(p1)
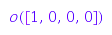

Now we can form linear combination of orbit sums:
p1 + 4*m
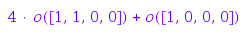
as well as products:
p1*m

As you can see, the result has been rewritten as a linear combination of orbit sums.
Actually, any invariant can be uniquely written as a linear combination of orbit sums (this follows easily from the fact that a group of permutations sends monomials to monomials). In particular, the basis of 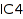 is indexed by the integer vectors of length
is indexed by the integer vectors of length 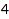 , considered up to a permutation in the cyclic group
, considered up to a permutation in the cyclic group 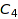 :
:
IC4::basisIndices

We have met above the symmetric powersum  . In fact, any symmetric polynomial is in
. In fact, any symmetric polynomial is in 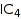 . Some simple ones can be directly constructed as follow:
. Some simple ones can be directly constructed as follow:
IC4::powersum(3)
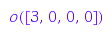
IC4::elementary(2)
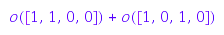
We now move on to the study of the invariant ring of 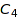 itself:
itself:
C4 := Dom::PermutationGroup(4, [[[1,2,3,4]]]):
IC4 := Dom::PermutationGroupInvariantRing(Dom::Rational, C4):
Some information on the ring is available right away, namely, it is of Krull dimension 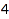 , it is non-Modular Cohen-Macaulay and not Gorenstein (we refer to the litterature for the definitions):
, it is non-Modular Cohen-Macaulay and not Gorenstein (we refer to the litterature for the definitions):
IC4::dimen;
IC4::isModular();
IC4::isCohenMacaulay();
IC4::isGorenstein()




An essential task when studying invariant rings is to find good degree bounds (an integer 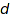 such that the ring is generated by invariants of degree less than
such that the ring is generated by invariants of degree less than 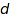 ). Aside from theoretical aspects, such degree bounds condition the complexity of many of the algorithms. In the non modular case, one can use Noether's degree bound given by the size of the group:
). Aside from theoretical aspects, such degree bounds condition the complexity of many of the algorithms. In the non modular case, one can use Noether's degree bound given by the size of the group:
IC4::degreeBound();
IC4::degreeLowerBound();
IC4::degreeBoundIsOptimal()



Without further computations, the system can not decide whether this degree bound is tight (in fact it is).
Generally speaking, this bound is always tight for cyclic groups, and never for all the other groups. The system uses a variety of other techniques to try to improve this degree bound, using successive refinements of Noether's theorem by Fleishmann, Schmid, Domokos, Hegedus, and Sezer, as well as degree bounds of Garsia, Stanton, and Goebel for the special case of permutation groups. However, most of the time, the degree bound is is still way of. If by chance you know in advance a good degree bound, you may specify it to the system with:
It is also relatively cheap to compute the Hilbert Series of  . This is the generating series of the homogeneous components of degree
. This is the generating series of the homogeneous components of degree 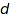 of the invariant ring. This is also the generating series of orbit sums by degree. It can be computed by means of the general Molien's formula. By default, it is computed by Pólya enumeration, which is faster:
of the invariant ring. This is also the generating series of orbit sums by degree. It can be computed by means of the general Molien's formula. By default, it is computed by Pólya enumeration, which is faster:
IC4::HilbertSeries()
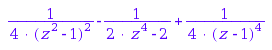
series(IC4::HilbertSeries(), z)
In characteristic zero, one may always take the symmetric powersums as primary invariants:
IC4::primaryInvariants()
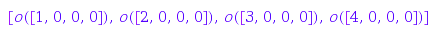
In case you know a better primary invariants (typically of lower degree), you may specify them using IC4::setPrimaryInvariants
Here is the Hilbert series of the free-subring generated by the primary invariants (here the symmetric functions):
IC4::primaryInvariantsRingSeries()

In the non modular case, the invariant ring is Cohen-Macaulay; in other words, it is a free module over the subring generated by the primary invariants. Generators for this module are called secondary invariants. Their generating series can be obtained at no cost as the quotient of the Hilbert series of the two rings:
normal(IC4::HilbertSeries()/IC4::primaryInvariantsRingSeries())
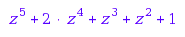
It is better thought to use directly the "secondaryInvariantsSeries" method (internally, the Hilbert series is in fact usually computed from the generating series of secondary invariants).
IC4::secondaryInvariantsSeries(z)
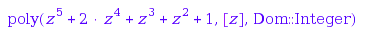
Now we turn to expensive computations. Here are the secondary invariants themselves:
IC4::secondaryInvariants()

This gives us a Hironaka decomposition of IC4. As a by-product, we get irreducible secondary invariants for IC4:
IC4::irreducibleSecondaryInvariants()

Together with the primary invariants, the irreducible secondary invariants form a reasonnably small homogeneous generating set of the invariant ring. To be precise, it is a generating set which is minimal among all generating sets containing the primary invariants.
Now, the information on the degree bound has been updated:
IC4::degreeBound();
IC4::degreeLowerBound();
IC4::degreeBoundIsOptimal()



We can also compute directly a minimal generating set; this is usually faster than computing a Hironaka decomposition:
IC4::minimalGeneratingSet()

Let us conclude with the ring  of symmetric polynomials in
of symmetric polynomials in 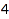 variables:
variables:
S4 := Dom::SymmetricGroup(4):
IS4 := Dom::PermutationGroupInvariantRing(Dom::Rational, S4):
It has a very nice Hilbert Series, which is also the generating series of partitions of 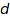 in at most
in at most  parts:
parts:
series(IS4::HilbertSeries(z), z, 8)
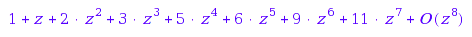
combinat::partitions::count(n, MaxLength = 4) $ n = 0..7

It is the polynomial ring over the elementary symmetric functions:
IS4::minimalGeneratingSet()

In particular,  has only one secondary invariant:
has only one secondary invariant:
IS4::secondaryInvariantsSeries(z)

IS4::secondaryInvariants()
Note that, for symmetric polynomials, the orbitsum basis is just the usual monomial basis. To compute with other bases (elementary, complete, Schur, ...), please refer to examples::SymmetricPolynomials.
In this last example, we do some computations in the modular case. Consider the invariant ring of 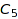 over
over  :
:
C5 :=Dom::PermutationGroup(5, [[[$1..5]]]):
IC5:=Dom::PermutationGroupInvariantRing(Dom::IntegerMod(5),C5):
As we are now in the modular case, we ca not decide right whether the ring is Cohen-Macaulay or Gorenstein. Also, Noether's degree bound does not apply anymore:
IC5::isModular;
IC5::isCohenMacaulay;
IC5::isGorenstein;
IC5::degreeBound()




The computation of a minimal generating set is now quite expensive because we need to do the full computation up to degree 10!
IC5::minimalGeneratingSet()

We finally get the expected degree bound of 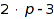 :
:
IC5::degreeBound()

The algorithm to compute Hironaka decomposition essentially works in the modular case. Of course, the invariant ring may not be Cohen-Macaulay, in which case the invariant ring is not a free-module over the primary invariants. The obtained secondary invariants still generate the ring as a module, but are not independent. Here is the number of secondary invariants per degree:
map(IC5::secondaryInvariants(), nops)

Note that there is one more secondary invariant of degree 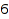 than the Hilbert series suggests:
than the Hilbert series suggests:
normal( IC5::HilbertSeries() / IC5::primaryInvariantsRingSeries() )
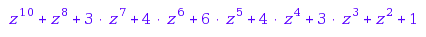
The algorithm has discovered the relation, and updated "isCohenMacaulay" appropriately:
IC5::isCohenMacaulay

Caveat: the algorithm does not use the Hilbert series to predict the number of secondary invariants at each degree, which is good. On the other hand, it still uses it as a stopping condition for the degree, which may be completely incorrect! So, please consider the result as a partial system of secondary invariants up to the degree of dom::secondaryInvariantsSeries():
![]() be a permutation group, that is a group acting faithfully by permutation on a finite set
be a permutation group, that is a group acting faithfully by permutation on a finite set ![]() (see Dom::PermutationGroup for details). Let also
(see Dom::PermutationGroup for details). Let also ![]() be a ring. The action of
be a ring. The action of ![]() extends naturally to a linear action on the ring of polynomials
extends naturally to a linear action on the ring of polynomials ![]() . The subspace
. The subspace ![]() of the polynomials which are invariant w.r.t. the action of
of the polynomials which are invariant w.r.t. the action of ![]() is an
is an ![]() graded algebra called the invariant ring of
graded algebra called the invariant ring of ![]() over
over ![]() .
.![]() , one can construct an invariant
, one can construct an invariant ![]() by summing all the monomials in the
by summing all the monomials in the ![]() -orbit of
-orbit of ![]() ; this invariant is called the orbit sum of
; this invariant is called the orbit sum of ![]() . The set of all orbit sums of monomials forms a vector space basis of
. The set of all orbit sums of monomials forms a vector space basis of ![]() .
.