The MuPAD-Combinat Handbook

The choice of the development platform was a difficult question; at some point, after long discussions, we had to take a decision. We try to present here why we were led to choose MuPAD. The table 1 summarizes how we evaluated several platforms with respect to our specifications for this project (see the specifications). This evaluation is based on our personal daily experience, in our field, with our programming and computing habits; we have tried to be as objective as possible, but we do not claim any kind of scientific rigor nor universality. We will also be glad to update it, if some readers explain to us why their favorite system has been underrated.

Rating of some platforms we investigated with respect to different aspects we judged of importance. Each rating ranges from F (worst) to A (best), ? meaning a lack of information. For example, is a full featured functional programing language and is rated A, whereas MuPAD does not support at all compilation of user code, and is rated F. For general purpose programming language, we tried to take into account open source or freely available libraries to build upon. This includes for example for , or and for .

A short summary is in order. The development cycle is too long in programming languages like , and there are not yet strong enough computer algebra libraries for our needs. We would have preferred to use a computer algebra system that was already widely used, in particular in the algebraic combinatorics community, like the commercial system or . However, the programming language, the license conditions, and the long term maintenance of are terrible. Technically, looks better, but does not seem to fit our technical requirements concerning object oriented features and overloading. Not going for the academic system was a tough choice, as they have an excellent open source development model and a clean programming language. What kept us from choosing it is that general computer algebra tools are missing. Still we want to collaborate closely with the team, for example for using as a group theory computation server. was not yet open-source at that time, and even today, its future seems still to be uncertain; aside from this, its language and design, together with the existence of the compiler, makes it an excellent candidate; in fact, many ideas in the design of MuPAD, like domains and categories, are borrowed from . is a computer algebra system in its own, but the computer algebra libraries are in construction. Again, its type system makes as one of the most interesting systems for our goals. Finally, was quite appealing, in particular for its impressive efficiency. However, we are afraid that their closed development model, with a lot of the work being done in C in the kernel, will not scale in the long run. Also it does not offer us the programming flexibility that we need.

Only the future will tell us if our choice of MuPAD was a right one. So far, after three years of development, the programming language has proved to fit well our needs, and the collaboration with the MuPAD group has worked out beautifully. Just to give a figure, in 2003, 400 out of the 1400 messages on the mupad-combinat-devel mailing list originated from the MuPAD team; this included code reviews, explanations on the internals of MuPAD, tips and tricks for optimizations, discussions on common developments that deserved to be synchronized, and so on.

Having our code deeply integrated in the MuPAD library is of great benefit for us. First, we gain in visibility, since our code is widely distributed. Second, it enforces high standards for code stability and documentation; though this is quite time consuming for us and imposes deadlines which are not necessarily compatible with our research schedule, this is essential for attracting new users. Also, our code and documentation are tested every night on the MuPAD servers as part of their standard test-suite. In this way, any incompatibilities are instantly detected. In particular, the MuPAD developers have to take our project into account before deciding any backward incompatible change that could break our code; if the change is still done, they are forced to either fix our code directly, or at least to provide us with timely information on how to do it ourselves. This is essential for the long term maintenance of our project. Reciprocally, some of our suggestions have had an essential impact in their decision for several small but critical kernel changes; this helped us to write cleaner and more efficient code.

Altogether, there is essentially one single aspect we are not happy with for the long term survival of , namely that MuPAD is not open-source. Still, they have kept so far their promises to remain relatively open. The situation has even improved recently with MuPAD Light being completely free (gratis) for research and education. They also have promised to release the code source of the library under a well known open-source license, some day.

Looking back at previous projects shows that the choice of a proper development model is essential for the long term survival of a project. In fact, the first months of the development of this project have been spent in large parts discussing this issue and trying out different solutions.

First, it is important that the core development be done by several persons with permanent positions to avoid the left-for-industry dreaded effect. Of course, this does not preclude students from writing libraries around this core, on the contrary! Also, code sharing code is time-consuming: seen over a short period, providing a polished implementation of a routine, with documentation and tests, represents much more work than just going for a write-once-use-once implementation. There, it is essential to reach quickly the critical mass of developers so that altogether they actually save time by participating to the project and benefiting from other's code.

In this spirit of sharing code and attracting new users and developers, going for an open source license was an obvious choice. Having an open platform would have helped as well. What is less obvious is how much the standard open source development models apply to the algebraic combinatorics community. The main problem is that this community is relatively small with not so many potential participants. The fact that participating in such a software requires the use of several standard open source management tools (cvs, make, Wiki) which are essential to automatize things may be seen as an additional difficulty. We try our best to leverage those difficulties, and the http://sourceforge.net support center is of great help for that. But still, some of those tools have a steep learning curve. Also, the structure of the package, which as been designed with genericity and extensibility in mind, is clear and systematic, but not so simple, and relies on non trivial programming concepts (generators, inheritance, ...).

As a consequence of this, and despite much documentation, advertising, and teaching efforts, we have not been as successful as we would have desired at attracting new users and developers. In particular, we have not yet quite reached the required critical mass. Another aspect of this is that the project is not yet as international and lab-independent as it ought to be to ensure its political independence. It seems that, so far, getting new developers started still requires a regular physical contact.

The convention for library, domain and function names is to use long names that are as meaningful and close to the English spelling as possible: e.g. partitions instead of PART, FreeQuasiSymmetricFunctions instead of FQSym, etc. In particular, abbreviations should be avoided, except in extreme cases where the short name is really well established (say Lex instead of Lexicographic). Here are the motivations for this convention:

We follow the capitalization rules of the MuPAD coding standard, which are quite similar to Java or C++ rules:

When the name of a library, domain or function is composed of several parts, and those parts are also used in other names, it may be worthwhile to order those parts from the most general to the most specific. For example, we used the name combinat::integerVectorsWeighted instead of the more natural name combinat::weightedIntegerVectors. The advantage is that all the domains dealing with integer vectors start with the same prefix, which is particularly practical with respect to automatic completion. This is also coherent with the hierarchy library::sublibrary::subsublibrary. Another typical case is when several functions return a similar result but under different forms; the function that is the most useful or natural gets the short name, and the names of the other functions, are suffixed with the "type" of the result (words::inversions/words::inversionsList, ...). We also used this rule of thumb for the names of the free module methods

The notion of combinatorial object is best described by some examples: a partition, a binary tree, a permutation, a graph, a Feynman diagram, a Dyck word, and other similar discrete objects are all combinatorial objects.

A combinatorial class is a (countable) set of related combinatorial objects (e.g. the set of all partitions, the set of all binary trees, the set of all standard permutations), on which a size function is defined (e.g. the size of partition is the sum

of its parts; the size of an integer vector consist of a pair

of integers: its sum

and its length

; the size of a tree is the number of its nodes). Typically, the fibers of the size function define natural finite subsets of the class that one wants to count, enumerate, and so on (e.g. counting all the partitions of

, listing all the integer vectors of sum

and length

); we say “typically”, because there are some cases where it is practical to use this framework even if the subsets are only countable. In many cases optional restrictions can be added to define smaller subsets of the class to be counted/enumerated/..., (e.g. the partitions of

of length at most

). In some combinatorial classes (e.g. the class of the permutations of

), the size function may be degenerated and have only one non trivial fiber.

A combinatorial object may belong to several combinatorial classes simultaneously. For example, the list [4,3,2,1] may be interpreted as a partition, a permutation, an integer vector, a composition. This is reflected in MuPAD by our convention that a combinatorial object is not necessarily strongly typed by the combinatorial class(es) to which it belongs. An object has a unique domain: it corresponds to the data structure of the object and can be obtained by the command domtype. On the other hand, it may be of different types: they correspond to the different semantics that can be attached to the object, and they can be tested with testtype.

For example, [3,4,2,1] belongs to the MuPAD domain of lists, DOM_LIST; it is simultaneously a list of positive integers (Type::ListOf(Type::PosInt)), a word, a permutation, etc, while it is not a partition:

testtype([3, 4, 2, 1], Type::ListOf(Type::PosInt)),

testtype([3, 4, 2, 1], combinat::words),

testtype([3, 4, 2, 1], combinat::compositions),

testtype([3, 4, 2, 1], combinat::integerVectors),

testtype([3, 4, 2, 1], combinat::permutations),

testtype([3, 4, 2, 1], combinat::partitions)

In the MuPAD terminology, the domains like combinat::compositions are called facade domains; they do not really contain elements of their own.

On the other hand, some combinatorial objects, such as trees, require a specific data structure; these objects are strongly typed, that is their domain is the class itself. This has, among others, the advantage that they are pretty printed by the system:

t := combinat::labelledBinaryTrees([1, [2], [3]]);

domtype(t);

testtype(t, combinat::labelledBinaryTrees);

/ \

2 3

This choice of not systematically using strong typing for combinatorial classes is not an obvious one, and there is no clear cut criteria for deciding whether a given combinatorial class should use strong typing or not. On the one hand, strong typing allows for object-oriented techniques and overloading. On the other hand, having to cope with all the conversions (a partition is also a composition, ...) can be quite a burden for both the user and the programmer; indeed, choosing which implicit conversions to provide is not an easy task, given the overwhelming number of natural bijections. Finally, with the current MuPAD language, there is a small memory and time overhead with strong typing; this can be considered as a misfeature of MuPAD though.

Aside from the data structure criteria, another reasonable criteria is whether the combinatorial class has natural “algebraic operations”. This is why we currently have both a facade domain combinat::permutations for general permutations seen as words, and a real domain Dom::SymmetricGroup for standard permutations seen as elements of the symmetric group. Actually, it could be reasonable to have a real domain Dom::Permutation, and have Dom::SymmetricGroup and Dom::PermutationGroup be facade domains for Dom::Permutation. This is still under discussion, and comments are welcome.

Combinatorial classes for which we want to do counting, generation, or other manipulations are represented by MuPAD domains, like combinat::partitions or combinat::binaryTrees. Note that, in many cases, those domains are just facade domains and do not really contain elements: as we said above, the domain of a partition, or of a permutation, is really DOM_LIST. Those domains also define a MuPAD type; by convention, it is named like combinat::partitions::type, and can be tested with:

testtype([3, 2, 2, 1], combinat::partitions)

Simpler combinatorial classes, which we only want to use for type checking, are just represented by MuPAD types. This is typically used for subsets of other combinatorial classes. For example, the standard permutations form a subset of all permutations, and are represented by the type combinat::permutations::typeStandard. We are not quite happy with this naming convention; however, for better localization, we really would like to keep the types defining a subset of a domain inside this domain. Another option was to use subdomains even in this case. But domains are quite special (and expensive?) objects in MuPAD: they have a reference effect, they cannot be deleted, etc. So, we feel that this would be overkill, especially for parametrized types like PermutationOf([a,b,c,d]).

Another related situation: quite often, we have a function that returns a collection

of related objects, usually as a list. Think of combinat::words::shuffle([1,2,3],[a,b,c]) which returns a list of words. Or think of the inverse of a function that is not at all injective like combinat::permutations::fromDescents (it returns all the permutations having a given descents set). In such cases, we often want to do some more involved things, like having a generator for the elements of

, or being able to count them without actually generating them. Then, it is natural to consider

as a combinatorial class, and to represent it by a MuPAD domain. This gives a unified interface to all the standard functions for counting, generating, ...:

As a nice side effect, the standard alias from new to list allows one to use the natural syntax combinat::words::shuffle(word1,word2) to obtain the collection

. So, switching from a simple function which returns

to a domain for the elements of

is transparent for the user. Usually, such a domain will be a subdomain of an existing domain (here combinat::words::shuffle is a subdomain of combinat::words).

A domain which represents a combinatorial class belongs to the category Cat::CombinatorialClass. Such a domain should implement at least generator or list. This category also provides naming conventions for usual functions like count, first, next, random, unrank, ... The implementation of those functions is not explicitly required by the category Cat::CombinatorialClass: depending on the specific combinatorial class sometimes they are not yet implemented, sometimes there exists no efficient algorithm, or sometimes they simply do not really make sense.

In the future, we may think about refining Cat::CombinatorialClass into subcategories that describe which of those functions are available (for example, the category of combinatorial class which provide an unrank function). So far, the benefits coming from such refinements do not seem to justify the overhead in the complexity of the category hierarchy.

Also, all of this is not really specific to combinatorial classes. We could imagine generalizing this to any kinds of collections of objects, and mimic the category hierarchy of, e.g. Aldor. By convention, all the subcategories of Cat::CombinatorialClass have a name of the form Cat::XxxClass. Right now, we have two sub categories of Cat::CombinatorialClass:

The name Cat::IntegerListsLexClass is too general, since this category contains only the combinatorial classes described using length, bound, and slope constraints. For example, the elements of combinat::permutations are integer lists and are naturally ordered lexicographically; however this combinatorial class is not in Cat::IntegerListsLexClass. Badly enough, we have not found a better name that would not be too long. Unless someone comes up with a clever suggestion we will stick to this name.

We use Next for the name of the method that computes the next element in a combinatorial class. This is not coherent with first, last and with the general convention that a method name start by a lowercase letter. Badly enough, next is a reserved keyword, and we cannot use it as method name in MuPAD.

Let us start by a precise definition for the term combinatorial algebra that we have used so far in a rather informal way.

Given a combinatorial class

, and a ring

, one can define the free module

with basis indexed by

over the ring

; an element of

is a formal finite linear combination of elements of

with coefficients in

. Alternatively, an element of

can be interpreted as a function from

with finite support; that is a function which is zero except on finitely many elements of the basis

For example, here is an element of the free module with basis indexed by partitions, over

Polynomials are another typical example of free modules, and we extend the usual definitions used for polynomials. The coefficient of

; we call the partition

, seen as an element of

, a term;

is a monomial; finally, the support of

is the set of the partitions with non-zero coefficients, that is

By combinatorial algebra we mean such a free module, together with some extra algebraic operations (a product, coproduct, antipode) which makes it an algebra, a bialgebra, or a Hopf algebra. Those operations are typically defined by linearity on the basis.

With this definition, we have distinguished a special basis of the combinatorial algebra. Most of the time, a combinatorial algebra (like the algebra of symmetric functions) will actually have several interesting basis (Schur functions, power-sum functions, ...), all of them indexed by

. The underlying free module remains the same, but the operations will vary accordingly. Changing from one basis to the other is one of the fundamental operations.

Traditionally in computer algebra systems (say with , or ), symmetric functions have been represented by symbolic expressions:

p[2]*p[1];

muEC::SYMF::Top(p[2]*p[1]);

muEC::SYMF::Tos(p[2]*p[1])

This is also the approach used for polynomials, and more generally for Ore-algebras in . This has several advantages:

Altogether, this approach is fine when there are very few combinatorial algebras; however it does not scale to a dozen predefined algebras (that's our short-term goal) plus myriads of user-defined algebras. In practice, this is one of the main reasons why the project stalled when defining many new algebras became a must.

It was time for a complete redesign and rewrite of the package. We will see that using strong typing allows for circumventing all those drawbacks, without loosing too much of the advantages. The choice of switching to MuPAD was largely influenced by the strong integration of their domains/axioms/category mechanism in their system, that allows for strong typing, and object-oriented techniques.

The first thing to do is to choose the internal data structure to store an element of a free module. There are different possible implementations without a clear cut advantage of one over the others (as a parallel, in C++ there exists two implementations of association tables: map using sorted lists and hash_map using hash tables). We provide several of them:

An element x is stored as an association table (DOM_TABLE). For example, here is the internal representation of an element x:

F := Dom::FreeModuleTable(Dom::Rational, combinat::partitions):

x := 4*F([3, 2, 1]) + 3*F([2, 1, 1]) + 1/4*F([1, 1, 1, 1]);

extop(x)

math

Since any MuPAD object can be used as index of a table, there is no restriction on the basis elements. Accessing the coefficient of a term is constant time.

The kernel polynomial objects of MuPAD (domain DOM_POLY) are stored in a sparse non-recursive way using sorted lists of monomials with a fixed number of variables. If one forgets about the product, this provides a sparse data structure which is both compact in memory and very fast for linear operations. Typically, the MuPAD sparse matrices (domain Dom::Matrix, former Dom::SparseMatrix) use univariate polynomials internally as internal representation for sparse column vectors.

Similarly, an element x of Dom::FreeModulePoly(R, Basis) is stored using a polynomial:

(F := Dom::FreeModulePoly(Dom::Rational, combinat::partitions);

x := 4*F([3, 2, 1]) + 3*F([2, 1, 1]) + 1/4*F([1, 1, 1, 1]));

extop(x)

math

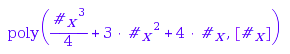
To achieve this, one needs to be able to represent an element of the basis using an exponent vector (an integer, or a fixed-length list of integers). This is trivial when the basis readily consists of fixed length lists of integers (integer vectors, standard permutations of a given

, Symbol::hellip). Otherwise, the user may provide a pair of functions rank and unrank that does the conversions. By default, the system creates a dummy pair of such functions: the rank function associate in turn the numbers 1,2,3,... to each new object it encounters. For example, the rank of [3,2,1], [2,1,1], and [1,1,1,1] above are respectively 1,2, and 3, that corresponds to the order in which the corresponding elements of F have been created.

This representation is very fast for linear operations. Furthermore, if univariate polynomials are used with the variable _X (this is the default), the data structure coincides exactly with the one used by Dom::Matrix. This allows for zero-cost conversions to and from sparse vectors, for doing linear algebra.

Accessing the coefficient of a term in an element x is logarithmic in the number of terms of x (in the multivariate case, with MuPAD < 3.0.0 this is linear instead of logarithmic).

Ranking and unranking is only done for conversions, and computing products. In practice, the overhead with the dummy implementation seems to be negligible, and largely compensated by the fact that most operations deal with integers.

Thanks to Stefan Wehmeier, (Univ. Paderborn) and Werner M. Seiler (Univ. Karlsruhe), this was mostly already implemented in the MuPAD library under the name Dom::FreeModule since 1997. An element is represented by a sorted list of terms. For example, here is the representation of the element x above: [[4, [3, 2, 1]], [3, [2, 1, 1]], [1/4, [1, 1, 1, 1]]].

Obviously, there needs to be an order on the basis elements (Basis should be a Cat::OrderedSet). Accessing a leading or trailing term is constant-time; accessing the coefficient of a given term in an element x is logarithmic in the number of terms of x.

All those implementations are in the category Cat::ModuleWithBasis which defines a unified interface. So, one can change the underlying implementation at any time. Unless you have a specific reason to choose one of the implementations, just use the default implementation Dom::FreeModule(R, Basis).

Once the underlying linear structure is implemented, it is very easy to construct functions on a free module by linearity / bilinearity / multilinearity on the basis (see the examples) using the utilities from operators. So, implementing operations like products, coproducts, antipodes usually boils down to implement the underlying combinatorics. Note that we do not have yet a general construction for the tensor product of two free modules F1 and F2, but you can emulate one by hand by building a free module whose basis elements are pairs of basis elements of F1 and F2.

Altogether, this allows to implement a domain F for the elements of a combinatorial algebra expanded on a given basis (e.g. the domain of symmetric functions expanded on the Schur functions, or the domain of symmetric functions expanded on the power-sum functions). The product of two elements of F is automatically expanded on the basis, and belongs again to F. Such a domain belongs to the category Cat::AlgebraWithBasis (later on, there will be categories such as Cat::BialgebraWithBasis, Cat::HopfAlgebraWithBasis).

A combinatorial algebra with several natural bases will be represented by several domains. Converting from one basis to another is an essential operation, and it is strongly desirable to be able to mix in the same expression elements that are expressed in different basis. This can now be achieved through overloading and the definition of appropriate implicit conversions (see the demonstration).

Developing the underlying tools that allow to do this seamlessly required a fair amount of work. Indeed, one parameter overloading in MuPAD works fine by delegating the work to the corresponding method of the parameter; on the other hand, the plain system essentially does not help much for multi-parameter overloading, which has to be carefully done by hand in each and every library (think about computing a product where the operands are in turn a symmetric function on the p basis, an integer, a symmetric function on the e basis, and a rational number). So we had to specify and implement a new mechanism that takes care of implicit conversions, and multi-parameters overloading. We essentially mimicked ideas taken from the GAP system GAP4, as well as from the static overloading mechanisms of standard languages like C++. The main difficulty was to choose the right level of generality, so as to make the system powerful enough, yet simple, safe, and sound. Our choices were largely influenced by our practical experience with the kind of computations we have in mind. This new overloading mechanism is being discussed for integration and systematic use in the MuPAD library. We are not at all specialists of this sensible subject, so comments and suggestions about this are very welcome. For details, see:

This mechanism is currently pretty rudimentary and limited. However, we have been playing with it intensively, and have done some really hairy stuff based on it. The semantic has proven so far to be safe, sound and robust, while really much more practical and powerful than the plain overloading mechanism. The time overhead is reasonable; if it became an issue, the specifications leave quite some room for optimisations, in particular by inclusion in the MuPAD kernel.

When defining combinatorial algebras with several bases, we organize the code in a fairly standardized way, which takes care of various technical issues such as initialization or parameterization of the algebra by the coefficient ring. We urge the interested reader to check out the code in the examples library, and in particular:

Having strong safeguards is essential so that a beginner can run computations with confidence. However, one of our motto is that the system should not try to be too clever, and in particular should always leave a way for the user to take over the control (and the responsibilities!). Indeed, there always are situations where the user knows that a given operation, invalid in general, happens to be perfectly legal in the current context. Most of the time, this can be taken care of by systematically providing conversions to and from symbolic expressions that the user may manipulate at his convenience. However, there is no clearly-defined representation of elements of non-commutative algebras using symbolic expressions, because MuPAD (as most other systems) assumes that the latter are commutative. Just to give a flavor of the issue: which commutation rules should be applied automatically by the system in the expression 2*e[1]*q*3*f[3]? Suggestions are very welcome here.

Throughout the tutorial, we have used fairly lengthy notations for constructing elements of combinatorial algebras. For example, to define the first symmetric power-sum, we wrote S::p([1]). This is fine in a tutorial when safety is at a premium, but in everyday's use, having terse notations is highly desirable. We are currently experimenting several tricks that allow for simultaneously using p to represent the domain of symmetric functions in the p basis, and p[1] for creating the first symmetric power-sum, while still being able to convert symmetric functions into symbolic expressions containing literals such as p[1]. As soon as we will have more experience with this, we will describe the recommended practice in the Tips and Tricks section of the reference manual.