Cat::IntegerListsLexClass

Cat::IntegerListsLexClass – the category of combinatorial classes based on combinat::integerListsLexTools

Cat::IntegerListsLexClass represents the category of combinatorial classes based on combinat::integerListsLexTools. It is used for lexicographic enumeration of list of integers verifying some constraints.

This is an internal category. It is used by the special purpose domains combinat::partitions, combinat::compositions, and combinat::integerVectors which provide user-friendly interfaces.

This documentation is only provided here for the curious reader as well as for developers. The interface is subject to incompatible changes anytime in the future. Use at your own risk.

Categories

Cat::CombinatorialClass, Cat::OrderedSet

Details:

This category provides an easy interface for combinat::integerListsLexTools. Refer to its documentation page for the description of the functionalities.
A Cat::IntegerListsLexClass is a set of list of non-negative integers sharing the same set of constraints.
Here, we call integer list a list l of nonnegative integers, its parts. By abuse of notation, infinite parts will be allowed in some cases. The length of l is the number of its parts; the sum of l is the sum of its parts.
Let minSlope be an integer or and maxSlope be an integer or . Then an integer list is regular w.r.t. minSlope and maxSlope if minSlope <= l[i+1]-l[i] <= maxSlope, for all i. Regular functions are defined similarly.
Let f be a function, and l an integer list. Then, f is an upper bound (resp. lower bound) for l if l[i]<=f(i) (resp. f(i)<=l[i]) for all i.
A set of constraints is specified by a sequence of objects: minLength, maxLength, floor, ceiling, minSlope, maxSlope with the following types:
- minLength: nonnegative integer;
- maxLength: nonnegative integer or +infinity;
- floor: regular function from [1..maxLength] to 0..+infinity;
- ceiling: regular function from [1..maxLength] to 0..+infinity;
- minSlope: integer or -infinity;
- maxSlope: integer or +infinity.
The purpose of the domains belonging to Cat::IntegerListsLexClass is to generate all the valid integer lists of a given sum which satisfy all the specified constraints.
A domain cl in Cat::IntegerListsLexClass must provide a procedure called parseOptions which takes an argument describing the constraints and returns the sequence of constraints as defined above. Then the category automatically implements the standard functions isA, count, list, generator, first, Next, last, previous and _less. For the description of these functions see Cat::CombinatorialClass.

Entries

"interfaceIntegerListsLexClass"

The standard common interface of a domain that belongs to Cat::IntegerListsLexClass. This is not really needed anymore.

Technical Methods

To help the writing of integers list classes, the following method is provided. It is not supposed to be called directly, but is rather here to provide default implementations.

parseOptionsIntegerListsLexClass – Parse the standard options of an integers lists Class.

Cat::IntegerListsLexClass::parseOptionsIntegerListsLexClass(t, c)

Parameters:

t:	A table of default constraints
c:	A sequence of constraints overriding the settings in t

Each constraint is given as an equation constraint=value where constraint is one of the following: MinLength, MaxLength, Length, MinPart, MaxPart, Inner, Outer, MinSlope, MaxSlope. The set of default constraints is given as a table of such equations. Extra constraints are also given as a sequence of such equations.

Here is a way to define the combinatorial class of vectors whose parts are zero or one, of given length and number of ones. As this category provides default implementations for the methods of a combinatorial class, we only need to provide the parseOptions function.

domain zeroOneVectors

inherits Dom::BaseDomain;

category Cat::IntegerListsLexClass;

parseOptions :=

proc(k)

begin

dom::parseOptionsIntegerListsLexClass

(table(Length = k,

MinPart = 0,

MaxPart = 1,

Inner = NIL,

Outer = NIL,

MinSlope = -infinity,

MaxSlope = infinity

),

args(2..args(0)));

end_proc;

end_domain:

Here is now the way to get the lists of such vectors of sum and length .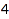

zeroOneVectors::list(2, 4)

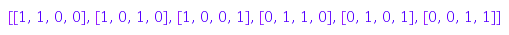
We now add constraints to force some parts to be equal to zero or one. This is now the way to get the lists of vectors of sum and length 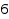, having zeros in positions 1 and 3 and ending with one.

zeroOneVectors::list(4, 8, Outer = [0, 1, 0, 1, 1, 1, 1, 1],

Inner = [0, 0, 0, 0, 0, 0, 0, 1])